Given a number $n$, then $P_k(n)$ is the number of ways to express $n$ as the sum of $k$ integers. For example $P_2(6)=7$
$0+6=6$
$1+5=6$
$2+4=6$
$3+3=6$
$4+2=6$
$5+1=6$
$6+0=6$
Now I worked out that $P_2(n)=n+1$ and $P_3(n)$ may be $P_3(n)=\sum^n _{k=0} P_2(n-k)$ but the question is:
Given $k$ and $n$ is there a formula to always find $P_k(n)$?
Yes, there is such a formula (assuming $k$ and $n$ are natural numbers).
In order to find it, I suggest you the following:
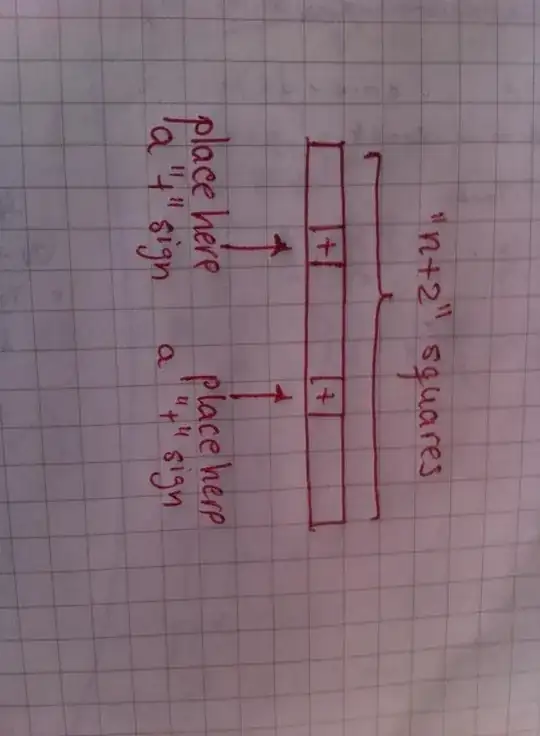
Let $k, n\in \Bbb N$. Suppose you have $n$ balls (representing the number $n$), what you want is the number of ways to place this $n$ balls on $k$ boxes (each box will represent the number being added), this can be encoded with a list of the balls, using vertical lines to separate the boxes.
For example, the partition $6=3+2+1$ can be encoded as
$$\bigcirc \bigcirc \bigcirc \mid \bigcirc \bigcirc \mid \bigcirc$$
Each partition correspond to a sequence of $n$ balls and $k-1$ separators, and each such a sequence correspond to a partition, so it suffices to count those sequences.
Those sequences are easy to count:
Those sequences consist of $n+k-1$ characters ($n$ balls and $k-1$ separators), just choose $k-1$ positions for the separators among all the $n+k-1$ available: $\binom {n+k-1}{k-1}$
If you have $a+b+c=n$ with $a,b,c,n$ positive integers, then the number of ways is $\left( \begin{matrix} n+2 \\ 2 \end{matrix} \right)$. wait and i'll make some latex draw to explain this:
The general formula is given by $$P_{k}(n) = \binom{n+k-1}{k-1}$$
For similiar reasons as in above Luis Felipe VillavicencioLopez's picture.
