For a periodic function we have: $$\int_{b}^{b+a}f(t)dt = \int_{b}^{na}f(t)dt+\int_{na}^{b+a}f(t)dt = \int_{b+a}^{(n+1)a}f(t)dt+\int_{an}^{b+a}f(t)dt = \int_{na}^{(n+1)a}f(t)dt = \int_{0}^{a}f(t)dt.$$ , but I don't understand how we obtain $\int _{b+a}^{\left(n+1\right)a}\:f\left(t\right)\:dt=\int _b^{na}\:f\left(t\right)dt$ in our equality?
Asked
Active
Viewed 313 times
0
-
1Is $a$ the length of one period? – Matthias Apr 16 '15 at 07:25
-
yes, a is the length of one period – Lucas Apr 16 '15 at 07:42
-
You add $a$ to both the lower and the upper limit. You start with $b$ and $na$ and end up with $b+a$ and $na+a=(n+1)a$. – mickep Apr 16 '15 at 07:54
-
and how we split that? can you show me ? how you split $\int _b^{na}:f\left(t\right)dt$ to obtain $\int _{b+a}^{\left(n+1\right)a}:f\left(t\right):dt$ ? – Lucas Apr 16 '15 at 07:57
3 Answers
3
If $a$ is the length of one period, then $f(t)=f(t-a)$ and so on. Then
$\int_{b+a}^{na+a}f(t)dt=\int_{b+a}^{na+a}f(t-a)dt=\text{(take $u=t-a$)}=\int_{b}^{na}f(u)du$
mathifold.org
- 939
-
-
@Lucas Well, $f(t)=f(t+a)=f(t+2a)=f(t+3a)=...=f(t-a)=f(t-2a)=...$ It's all the same. – mathifold.org Apr 16 '15 at 08:11
-
-
$\int _b^{b+a}:f\left(t\right):dt=\int _0^a:f\left(t\right)dt$ is general case for a periodic functions? – Lucas Apr 16 '15 at 08:15
-
@Lucas This would be true if the period is $b$. Translations not related to the period do not preserve the function and neither the integral. – mathifold.org Apr 16 '15 at 08:21
2
Let $F$ be a primitive of $f$. Then, by the fundamental theorem of calculus, one has
$ \frac{d}{db} \int_{b}^{b+a}f(t)dt= \frac{d}{db} [F(b+a)-F(b)]=F^ \prime (b+a)-F^ \prime (b)=f(b+a)-f(b)=0.$
since $f$ is $a$-periodic. Then, the integral $\int_{b}^{b+a}f(t)dt$ is independent of $b$, so one can take $b=0$.
Idris Addou
- 4,223
-
Thank you,but I want to understand something else, how we demonstrate that $\int _{b+a}^{\left(n+1\right)a}:f\left(t\right):dt$ is equal with $\int _b^{na}:f\left(t\right)dt$ ? – Lucas Apr 16 '15 at 22:26
-
This is a simpler question: it suffices to perform the change of variable $u=t-a$ in your right hand integral, you will got the left one after using the fact that $f$ is $a$-periodic, namely $f(t-a)=f(t)$. – Idris Addou Apr 16 '15 at 22:36
-
I know that was a simple question, but is my first time after a long time when I comeback to "play math", I forgot some things.. :D – Lucas Apr 16 '15 at 22:42
1
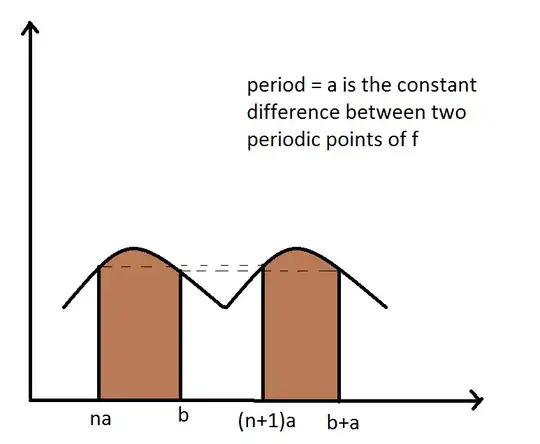
What does it mean for a function to have a period $a$ ? Informally, it means that the function values gets repeated after an increment of $a$ in the $x-$value. (domain value). Notationally,
$$a\textrm{ is period of }f\iff f(x)=f(x+a)~\forall~x,x+a\in\textrm{Dom(f)}$$
That gives us $na=na+a=n(a+1)$ and $b=b+a$ since $na$ and $b$ are domain values ($x-$values) for $f$ and $a$ is the period.
So, the definite integral remains the same.
Here's a simple diagram:
Prasun Biswas
- 6,417
-
$\int _b^{b+a}:f\left(t\right):dt=\int _0^a:f\left(t\right)dt$ is general case for a periodic functions? – Lucas Apr 16 '15 at 08:14
-
-
-
-
-
