The following problem is a detail from a proof I wrote recently -- a detail that I left unproven, and would like to prove.
Let there be three points $a$, $b$, and $c = \frac{a+b}{2}$, with $a<b$. We have a function $f$ such that $f(a) < f(c) \leq \frac{f(a)+f(b)}{2} < f(b)$.
So we can draw a line from $(a,f(a))$ to $(b,f(b))$ and the point $(c,f(c))$ will be on or below that line.
We then claim that the slope of the line from $(a,f(a))$ to $(c,f(c))$ is less than or equal to the slope of the line from $(c,f(c))$ to $(b,f(b))$. Why is this true? The intuition is clear to me, but I don't know how to formalize this.
A diagram below for clarity.
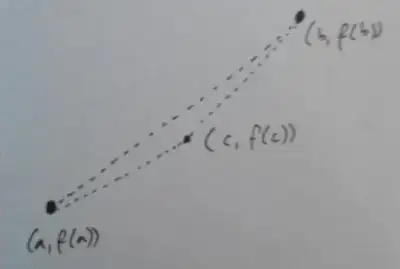
No matter how we place $f(c)$, the point $(c,f(c))$ will clearly always be such that the slope from $(a,f(a))$ to $(c,f(c))$ is less than the slope from $(c,f(c))$ to $(b,f(b))$ -- if this were not the case, then the point $(c,f(c))$ would have to lie above the line from $(a,f(a))$ to $(b,f(b))$. But how do I prove this?