Given a rectangle of integer sidelengths $m\times n$, consider partitioning it into smaller rectangles also of integer sidelengths. How many such partitions are possible?
I wonder if this is just an exercise-level problem or something that hasn't been solved... it is such a simple question that was probably studied before.
There is a nice discussion of a more simple problem here: Number of ways to partition a rectangle into n sub-rectangles Given its complexity, I have doubts that your problem has a nice closed-formed answer.
We consider the rectangle $R_{mn}:=[0,m]\times[0,n]$ as a band of "small" width $m$, fixed once and for all, and variable height $n$. Denote the number of partitions of $R_{mn}$ into subrectangles by $P(n)$.
Any partition of $R_{m,n+1}$ reduces to a partition of $R_{mn}$ when the topmost row of little squares is chopped off. But each partition of $R_{mn}$ can be extended to a partition of $R_{m,n+1}$ in various ways, depending on the inner vertical edges present (i.e., used for separating two subrectangles) in the top row of $R_{mn}$. There are $m-1$ inner edges, allowing for $N:=2^{m-1}$ different patterns of present edges. Let $p_k$ $\>(1\leq k\leq N)$ be the pattern defined by the binary expansion of $k-1$.
Assume that pattern $p_k$ is present in the top row of $R_{mn}$. Then a priori any pattern $p_j$ can be selected for the $(n+1)^{\rm th}$ row. When the two patterns are aligned most top rectangles of $R_{mn}$ cannot be extended upwards in an admissible way, but a certain number $s=s_{jk}\geq0$ of them can. For each of these we can choose to extend or not, making a total of $2^s$ choices.
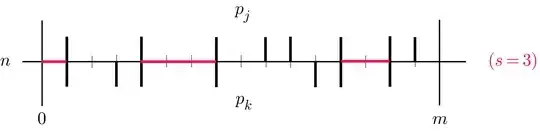
The numbers $s_{jk}$ depend on the patterns $p_j$, $p_k$ under consideration and have to be determined in a preparatory step. The $s_{jk}$ give rise to transition matrix $Z$ of type $N\times N$ as follows: $$z_{jk}=2^{s_{jk}}\qquad(1\leq j\leq N, \ 1\leq k\leq N)\ .$$ Denote the number of partitions of $R_{mn}$ having pattern $p_k$ in its top row by $x_k(n)$. Then $$x_k(1)=1\qquad(1\leq k\leq N)\ .$$ We now have the recursion $$x_j(n+1)=\sum_{k=1}^N z_{jk}x_k(n)\qquad(n\geq1)\ ,$$ in short: $${\bf x}(n+1)=Z\>{\bf x}(n)\ .$$ This finally gives $$P(n)=\sum_{k=1}^N x_k(n)\ .$$ Two examples: Letting $m=4$ the matrix $Z$ is given by
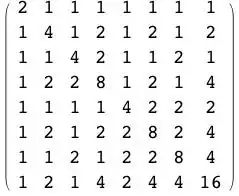
and produces $$P(10)=Z^9(1,1,1,\ldots,1)^\top=10\,225\,294\,476\,962\ .$$ For an $8\times 8$ chessboard one obtains $$3\,250\,879\,178\,100\,782\,348\,462$$ partitions into rectangles.
