8

I am trying to understand the genus of an algebraic curve in the complex plane $\mathbb{C}P2$. I am looking for a visual or intuitive understanding. The difference between a sphere and a torus as a surface of genus 0 and 1 resp. is clear, but how does the surface relate to the planar curve?

As an example take the following parametrization: $$ t \in \mathbb{C} \mapsto (x,y,z) := (t+t^3, t-t^3, 1+t^4) \in \mathbb{C}P2 $$ Where $(x,y,z)$ are complex homogeneous coordinates, i.e. $(x',y') := (x/z, y/z) $ would be "normal" complex coordinates.

The parameter $t$ is $\in \mathbb{C}$ so one may regard the parameter $t$ on a Riemann sphere, where some points on the sphere are singular.

Is that the reason the genus of this curve is $0$, because it has a parametrization on a Riemann sphere?

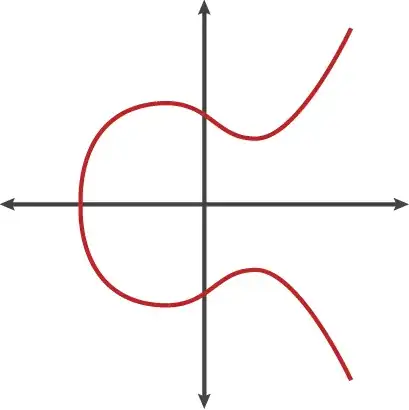
Wikipedia claims that the Cassini ovals are curves of genus 1.
However the lemniscate is of genus 0.
I am inclined to believe that the Cassini oval looking like an ellipse is also genus $0$. Is that correct?
It could be that the Cassini oval consisting of two seperate parts is of genus 1. Is one part of the two seperate ovals then of genus $0$?

Gerard
  • 1,651
  • 4
    It is difficult to judge the genus of a complex curve from the shape of its points with real coordinates. An awful lot is missing. Also the compactification (automatic in $\Bbb{C}P^2$). The ellipctic curves are a case in point. The set of real points may even have two connectivitiy components.There are some (IIRC helpful) figures in an early chapter of Kendig's Elementary Algebraic Geometry. – Jyrki Lahtonen Apr 01 '15 at 13:17
  • Related: https://math.stackexchange.com/questions/163356 – Watson Nov 13 '16 at 17:32

1 Answers1

6

Since ${\Bbb C}$ is algebraically closed, a curve being rational (parametrisable) is equivalent to being of genus zero.

To be more visual, rational curves were called unicursal because you can draw them over the reals in one movement without leaving the paper. But be careful there are genus 1 curves that can be drawn like that too:

section of torus

The genus–degree formula relates the degree $d$ of a non-singular plane curve $C\subset\mathbb{P}^2$ with its arithmetic genus g via the formula: $g=\frac12 (d-1)(d-2) . \,$ If the curve is non-singular the geometric genus and the arithmetic genus are equal, but if the curve is singular, with only ordinary singularities, the geometric genus is smaller. More precisely, an ordinary singularity of multiplicity r decreases the genus by $\scriptstyle \frac12 r(r-1)$.

The Cassini ovals have double points at the circular points at infinity. We need three singular points to get down from genus three of a nonsingular quartic curve, so the ones with no extra node are of genus 1.

Jan-Magnus Økland
  • 6,019
  • This explains why the lemniscate is of genus 0, while the others are of genus 1. – Gerard Apr 01 '15 at 14:30
  • How about the relation of the other Cassini curves to the Riemann sphere? Apparatnly they cannot be parametrized - or? – Gerard Apr 01 '15 at 14:31
  • Your first sentence is rather complex, how on earth may that be visualised, or: is there any connection of that remark to the Riemann sphere? – Gerard Apr 01 '15 at 14:35
  • @Gerard The genus 1 curves cannot be parameterised by rational functions, no. Such a parameterisation would make the doughnut isomorphic to the sphere. – Jan-Magnus Økland Apr 01 '15 at 15:01