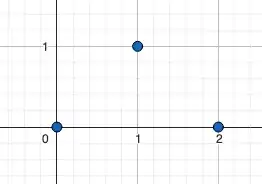
A simpler discrete example: Let $(X,Y)$ take values $(0,0)$, $(1,1)$, and $(2,0)$ with equal probability. Then:
$E(XY)= 0\cdot 0\cdot \frac13 + 1\cdot 1\cdot\frac13 + 2\cdot0\cdot\frac13=\frac13$
$E(X) = 0\cdot\frac13 + 1\cdot\frac13 + 2\cdot\frac13 = 1$
$E(Y) = 0\cdot\frac13 + 1\cdot\frac13 + 0\cdot\frac13=\frac13$
so that $\operatorname{Cov}(X,Y)=E(XY)-E(X)E(Y)=0$ and the correlation between $X$ and $Y$ is zero. This zero correlation quantifies the fact that the relationship between $X$ and $Y$ exhibits no linear trend either upward or downward.
However, $X$ and $Y$ are not independent. Here are two ways to argue:
- $P(X=1,Y=1)=\frac13\ne \frac13\frac13=P(X=1)P(Y=1)$.
- Given $X=1$, you know $Y=1$ for sure, so that $P(Y=1\mid X=1)=1$. This differs from the unconditional probability $P(Y=1)=\frac13$.
Three possible values for the pair $(X,Y)$ is the simplest situation where discrete random variables can be uncorrelated but not independent. When the pair $(X,Y)$ takes two possible values and $X$ and $Y$ are uncorrelated, then they are also independent.
Proof: Since covariance is preserved under translation, wlog we may assume $(X,Y)$ takes value $(a,b)$ with probability $p\ne0$ and value $(0,0)$ with probability $q:=1-p\ne0$. Compute $E(XY)=abp$, $E(X)=ap$, $E(Y)=bp$, and $\operatorname{Cov}(X,Y)=abpq$. If the covariance equals zero, then either $a=0$ or $b=0$. If $a=0$ then $b\ne0$ and $P(X=0)=P(X=a)=1$ while $P(Y=b)=p$ and $P(Y=0)=q$. Hence $P(X=0,Y=0)=P(X=0)P(Y=0)$ and $P(X=a,Y=b)=P(X=a)P(Y=b)$ and we have independence. The case $b=0$ is similarly proved; or argue by symmetry, swapping $X,a$ with $Y,b$.
