15

I know that a Binomial Distribution, with parameters n and p, is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p.

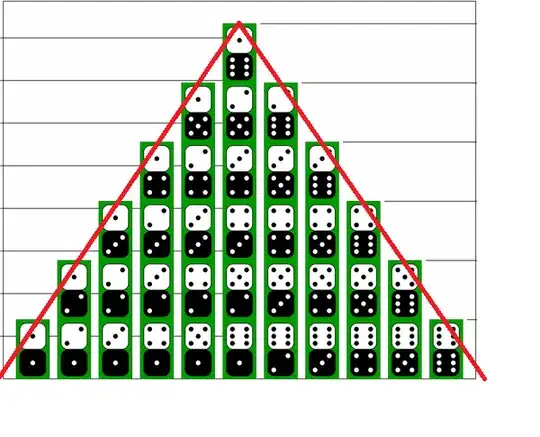
I read that the sum of the roll of two dice is a binomial distribution. Is this right? I know that the sum looks like a binomial:

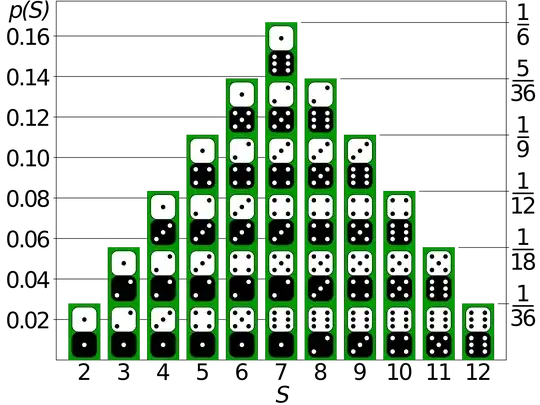
binomial dice rolls

But if it is a binomial :

  1. What event do I regard as a success?
  2. What is its probability?
  3. How many times do I repeat the experiment?

I mean a Binomial Distribution measures the probability of observing an event (which has probability of success p), k times in specific amount of repetitions n. Here I see 12 different events with different probabilities and I am confused.

Reinderien
  • 194
Stelios Avramidis
  • 165
  • how did you create the image? is there any site that does that? – Robson May 27 '15 at 10:21
  • Just found it one the internet sorry :( – Stelios Avramidis May 27 '15 at 21:17
  • 1
    Nitpick: "dice" is already a plural. "Two dices" is ungrammatical. The word "dices" does exist, but as a verb conjugation, as in "He dices the onions." – Dan Jun 10 '22 at 14:55
  • 2
    I know this is an old question but I stumbled on it looking for some good examples for my students. I think part of the problem here is in the form of your question and conflating it with what you've read. What you're probably referring to is that the sum of two dice being thrown to a specific sum over a number of trials is a binomial experiment. If you say, "sum of two dice equaling 6 in X number of trials", you meet all the criteria for a binomial experiment. A. you find it or you don't B. Each trial is independent C. The probability of success is always the same D. Trials are independent. – Dan Sep 17 '22 at 19:35

2 Answers2

16

TLDR: The sum of two $n$-sided dice is not binomially distributed.

A discrete random variable, $X$, has a binomial distribution, $X\sim Bin(n,p)$ when $Pr(X=x) = \begin{cases}\binom{n}{x}p^x(1-p)^{n-x}&\text{for}~x\in\{0,1,2,\dots,n\}\\ 0 & \text{otherwise}\end{cases}$

For $X$ the sum of two $n$-sided dice however, $Pr(X=x) = \begin{cases} \frac{n - |x-(n+1)|}{n^2} & \text{for}~x\in\{2,3,\dots,2n\}\\ 0 & \text{otherwise}\end{cases}$

Notice that since $n$ will be a fixed number, $Pr(X=x)$ is linear on the intervals $[2,n+1]$ and again linear on the intervals $[n+1,2n]$. This is in direct contrast to the binomial distribution scenario where $Pr(X=x)$ is definitely not linear (as it has terms like $p^x$ and $\binom{n}{x}$ appearing in the formula).

As mentioned in the comments above, as $n$ grows large, the histogram for the sum of two $n$-sided dice approaches the shape of a triangle.

enter image description here

This becomes even more apparent as $n$ gets even larger. Here is the start of the histogram for $n\approx 30$ (its a lot of effort to complete, but you get the idea).

enter image description here

On the other hand, the binomial distribution appears with the all-familiar "bell-shaped" curve.

enter image description here

As such, these are two very different distributions and should not be confused.

JMoravitz
  • 80,908
  • This is an excellent and descriptive answer, thank you. – Stelios Avramidis Mar 24 '15 at 19:27
  • 1
    This answer is at odds with Wolfram's article on Dice, which shows that the distribution of totals as the number of dice rolled increases does approach a binomial distribution. – RBerteig Jun 07 '17 at 21:43
  • 7
    @rberteig if you read more closely, the $ n $ i refer to here is the number of sides, not the number of dice. The question was about the sum of specifically two dice. Yes, as the number of dice increase it will approach a normal distribution but that is irrelevant. – JMoravitz Jun 07 '17 at 22:11
5

No, this is not a binomial distribution. For one thing, a binomial distribution would have $P(X=0) > 0$.

Robert Israel
  • 470,583