6

Let $\triangle ABC$ be an acute-angled triangle. Let $H$ be the foot of the perpendicular from A to BC. Let $K$ be the foot of the the perpendicular of $H$ to $AB$, let $L$ be the foot of the perpendicular from $H$ to $AC$. Let $AH$ intersect the circumcircle of $ \triangle ABC$ in $T$, and let the line through $K$ and $L$ intersect the circumcircle of $\triangle ABC$ in $P$ and $Q$. Prove that $H$ is the incenter of $\triangle PQT$.

enter image description here

Jack D'Aurizio
  • 361,689
steedsnisps
  • 685
  • 1
    You seem to be using same names for both points and lines. Could you clarify what is what in this problem? – Wojowu Jan 05 '15 at 22:26
  • Ah yes, I'll edit it – steedsnisps Jan 05 '15 at 22:31
  • You must assume that $\triangle ABC$'s non-acute angle, if any, is at $A$. If $B$ or $C$ is obtuse, then $H$ is actually an excenter of $\triangle PQT$. – Blue Jan 06 '15 at 10:48
  • @Blue yes, can you solve it? – steedsnisps Jan 06 '15 at 10:55
  • 1
    @wowlolbrommer: I haven't solved it yet. Where did you get this problem? From a textbook, or perhaps from a contest? Knowing the difficulty level could be helpful in deciding how to approach the problem. – Blue Jan 06 '15 at 10:57
  • I found it in a training booklet for geometry. It is from the Russian Sharygin competition, but I cannot find the solution online. – steedsnisps Jan 06 '15 at 11:44
  • @Blue, are you making any progress with this problem. i have made some progress but with heavy trig. – abel Jan 06 '15 at 23:54
  • @abel: I have a brute-force coordinate argument that gets me somewhere, but I'm not yet seeing the good approach. – Blue Jan 07 '15 at 00:30
  • @Blue, i don't think this is true. – abel Jan 07 '15 at 02:56
  • @abel: My (and @Jack's) GeoGebra sketches demonstrate that the result is (probably) true. My coordinates-based argument proves the result, but right now it's too ugly to present. – Blue Jan 07 '15 at 03:20
  • @Blue, if you have time, can you please check my work. – abel Jan 07 '15 at 04:37

1 Answers1

4

In any triangle the orthocenter and the circumcenter are isogonal conjugates. Since $AKHL$ is a cyclic quadrilateral, this implies that the perpendicular to $PQ$ through $A$ passes through the circumcenter of $ABC$, $O$. This implies $\widehat{POA}=\widehat{AOQ}$, so $\widehat{PTA}=\widehat{ATQ}$, and $AP=AQ$. Let $A'$ be the symmetric of $H$ with respect to $A$. If we manage to prove $AP=AH$, then the perpendicular $l_P$ to $HP$ through $P$ and the perpendicular $l_Q$ to $HQ$ through $Q$ meet on $A'$, so $PTQ$ is the orthic triangle of the triangle $\Delta$ delimited by $l_P,l_Q$ and the perpendicular $l_T$ to $HT$ through $T$. This gives that $H$ is the orthocenter of $\Delta$, hence the incenter of $PTQ$.

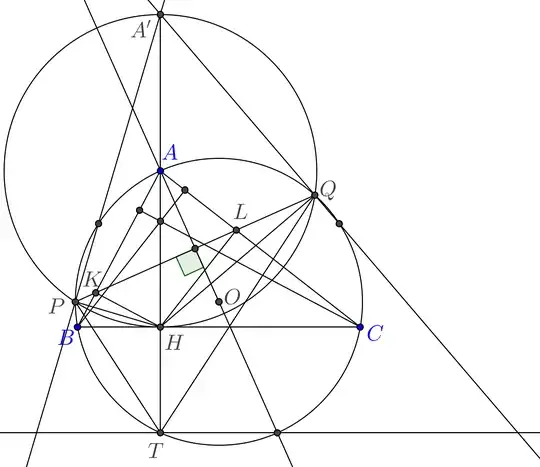
enter image description here

The best way I found so far to prove $AP=AH$ is to use some trigonometry, but I think there are more clever ways.

Edit: Thanks to wowlolbrommer, here it is a clever way: $AP=AQ$ implies $\widehat{AQL}=\widehat{ACQ}$, hence $AQ^2=AL\cdot AC$. By Euclid's first theorem, $AL\cdot AC = AH^2$, hence $AP=AQ=AH$ and we're done.

Community
  • 1
Jack D'Aurizio
  • 361,689