How to solve $\int_0^{\infty}\frac{\cos{ax}}{x^3+1}dx$?

Question

QUESTION. It is looked for a closed solution for following real integrals

$\displaystyle\int_0^{\infty}\displaystyle\frac{\cos{ax}}{x^3+1}dx$ and $\displaystyle\int_0^{\infty}\displaystyle\frac{\sin{ax}}{x^3+1}dx$

while the constant $a$ can be of any value; not only $a = 0$ or $a \rightarrow \infty$.

To explain the meaning of $a$, the first integral is considered in a practical context. The integral can be used to describe the stress distribution in flanged beam near a loading point where $r$ describes the stiffness of the flange, $F$ is a single force and $t$ is the wall thickness of the web. For the stress at the web's top it holds:

$\sigma = \displaystyle\frac{F}{\pi t r} \displaystyle\int_0^{\infty}\displaystyle\frac{\cos{\frac{d}{r}x}}{x^3+1}dx$

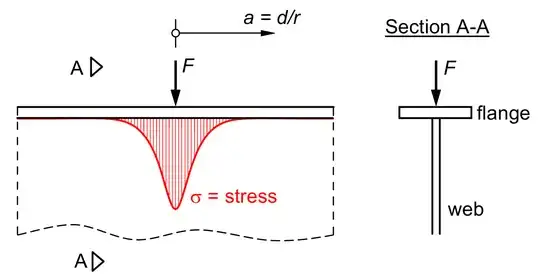
For a distance far remote from the loading point (meaning $a = d/r = \infty$), the stress (as the integral) will amount zero. In contrast the stress (as the integral) is maximum for $a = d/r = 0$. In this case the $\cos$-function drops out. By contour integration one gets

$\displaystyle\int_0^{\infty}\displaystyle\frac{dx}{x^3+1} = \frac{2\pi\sqrt{3}}{9}$

To describe the stress distribution as a whole the knowledge of the integral for any value $a$ is required.

TRIED SOLUTION. I try to solve the aforementioned real integrals considering the following complex integral

$\displaystyle\oint_C f(z)\,dz = \displaystyle\oint_C\displaystyle\frac{e^{iaz}}{z^3+1}\cdot \log{z}\, dz= \displaystyle\oint_C\displaystyle\frac{\cos{az}}{z^3+1}\cdot \log{z}\, dz+ i \displaystyle\oint_C\displaystyle\frac{\sin{az}}{z^3+1}\cdot \log{z}\, dz$

I know that such an approach is appropriate for the integration of $\frac{1}{x^3+1}$ within the same limits.

By $\log{z}$ the considered complex-valued function $f(z)$ gets a branch point at $z = 0$. This point is connected with $+\infty$ to form a branch cut. The contour $C = C_1\cup C_2 \cup C_3 \cup C_4$ does not cross the branch cut (see picture).

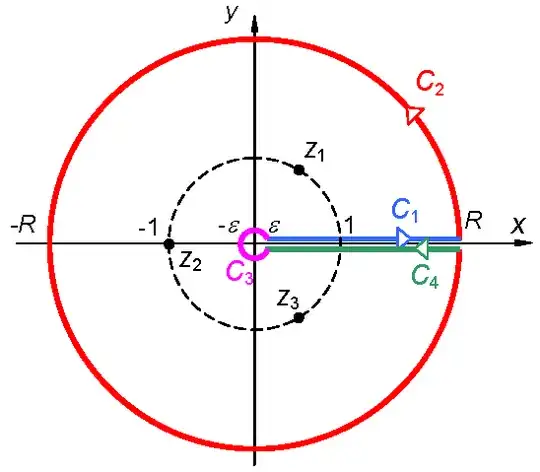
As the complex-valued function contains three poles $z_k$ inside $C$ it holds:

$\displaystyle\oint_C\displaystyle\frac{e^{iaz}}{z^3+1}\cdot \log{z}\,dz = 2\pi i \displaystyle\sum_{k = 1, 2,3}{\operatorname{Res} f(z): z_k}$

Looking at the paths it can be stated:

• Path $C_2$: integral tends to zero for $R \rightarrow\infty$ (Jordan's Lemma)
• Path $C_3$: integral tends to zero for $\varepsilon \rightarrow 0$ (can be proven)

• Paths $C_1$ and $C_4$ would cancel out each other if the considered complex-valued function did not contain $\log{z}$. Through $\log{z}$ both paths differ by their imaginary parts.

  Path $C_1$: $\log{z} = \ln{r} + i \cdot 0$

  Path $C_4$: $\log{z} = \ln{r} + i \cdot 2\pi$

After extending the integrals for $C_1$ and $C_4$ I end up with:

$\displaystyle\oint_C\displaystyle\frac{e^{iaz}}{z^3+1} dz = - \displaystyle\sum_{k = 1, 2,3}{\operatorname{Res} f(z): z_k}$

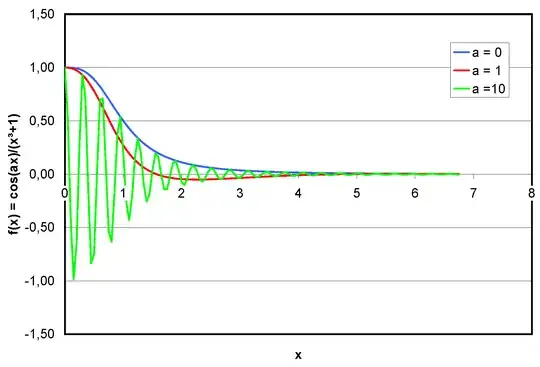
I know for sure that the real integrals that I am looking for tend to zero for high values $a$ due to the oscillation, see picture. But my solution does not. I fear my approach is not correct. I would deeply appreciate any comment or hint.

REMARK #1: I want to add some information on parity for the sake of completeness as Lucian raised that issue although this approach did not turn out to be successful for my case.

I split the original function into an even and odd part.

$f(x) = f_{even}(x) + f_{odd}(x)$

$\displaystyle\frac{\cos{ax}}{x^3+1}= -\displaystyle\frac{\cos{ax}}{x^6-1}+\displaystyle\frac{x^3\cos{ax}}{x^6-1}$

This led to following integral:

$\displaystyle\int_0^{\infty}\displaystyle\frac{\cos{ax}}{x^3+1}dx = \displaystyle -\frac{1}{2}\int_{-\infty}^{+\infty}\displaystyle\frac{\cos{ax}}{x^6-1}dx + \displaystyle\int_{0}^{+\infty}\displaystyle\frac{x^3\cos{ax}}{x^6-1}dx$

The different integration limits can be attributed to the symmetrical properties of the even function (meaning that integral from $-\infty$ to 0 equals integral from 0 to $+\infty$) that makes things easier.

I did the same splitting for the complex-valued function and chose the two contours shown in the picture.

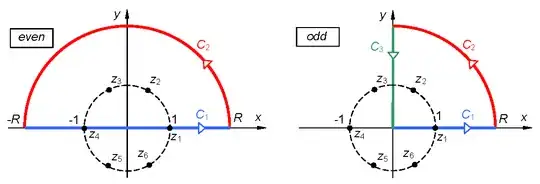
The integration of the even function along $C$ can be easily done as the integral of path $C_2$ dies out for $R \rightarrow\infty$ (Jordan's Lemma - here it holds indeed). For pole $z_1$ only half of the residuum has to be account for, as this pole is located on the boundary of the considered contour.

When integrating the odd part, the integral along path $C_2$ vanishes for $R \rightarrow\infty$ (similar to Jordan's Lemma), too. But the contribution of path $C_3$ cannot be neglected, unfortunately.

REMARK #2: Differentiation under the integral sign using the third derivative

I generalize the integral by introducing a parameter $b$:

$I(b) = \displaystyle\int_0^{\infty}\displaystyle\frac{\cos{ax}}{x^3+1}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right)dx$

For $b = 0$ I get the integral that I am looking for.

Now I determine the third derivative with respect to $b$ hoping that it turns into an expression that can be easily integrated with respect to $x$. As $\displaystyle\frac{\cos{ax}}{x^3+1}$ is considered as a constant while deriving with respect to $b$ I end up with

$\displaystyle\frac{d^3I(b)}{db^3} = \displaystyle\frac{d^3}{db^3}\displaystyle\int_0^{\infty}\displaystyle\frac{\cos{ax}}{x^3+1}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right)dx = \displaystyle\int_0^{\infty}\displaystyle\frac{\cos{ax}}{x^3+1} \frac{\partial^3}{\partial b^3}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right)dx$

Auxiliary calculations:

• $\displaystyle\frac{\partial}{\partial b}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right) = \frac{x^3b^2}{2}+\frac{b^2}{2}$
• $\displaystyle\frac{\partial^2}{\partial b^2}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right) = x^3 b+b$
• $\displaystyle\frac{\partial^3}{\partial b^3}\left(\frac{x^3b^3}{6}+\frac{b^3}{6} +1\right) = x^3 +1$

That gives a third derivative that does not converge.

$\displaystyle\frac{d^3I(b)}{db^3} = \displaystyle\int_0^{\infty}\cos{ax}\,dx = \left[\frac{1}{a}\sin{ax} \right]^{\infty}_0$

To conclude: although the used generalized integral does not seem to be appropriate, remark #2 regards the problem from a different angle that might be helpful for further discussions. Thanks to all contributors.

Answer 1

The problem with the initial approach is that along $C_2$, $\dfrac{e^{iaz}}{x^3+1}$ does not vanish as $R\to\infty$. For $a\gt0$, it vanishes in the upper half-plane, but blows up exponentially in the lower half-plane.

---

Convert from Oscillating to Monotonic Integral

Let's compute the integral of $\dfrac{e^{iaz}}{z^3+1}$ over $\gamma$, where $$ \gamma=[0,R]\cup Re^{i[0,\pi/2]}\cup[iR,0]\tag{1} $$ The integral of $\dfrac{e^{iaz}}{z^3+1}$ along $Re^{i[0,\pi/2]}$ is less than $\frac{R\pi/2}{R^3-1}$ which vanishes as $R\to\infty$.

The residue of $\dfrac{e^{iaz}}{z^3+1}$ at $z=e^{i\pi/3}$ is $\frac13e^{-a\sqrt3/2}\left[\cos\left(\frac a2-\frac{2\pi}3\right)+i\sin\left(\frac a2-\frac{2\pi}3\right)\right]$.

Since $z=e^{i\pi/3}=\frac12+i\frac{\sqrt3}2$ is the only singularity inside $\gamma$, we get $$ \begin{align} &\frac{2\pi i}3e^{-a\sqrt3/2}\left[\cos\left(\frac a2-\frac{2\pi}3\right)+i\sin\left(\frac a2-\frac{2\pi}3\right)\right]\\ &=\int_\gamma\frac{e^{iaz}}{z^3+1}\mathrm{d}z\\ &=\int_0^\infty\frac{e^{iax}}{x^3+1}\,\mathrm{d}x-i\int_0^\infty\frac{e^{-ax}}{1-ix^3}\,\mathrm{d}x\\ &=\int_0^\infty\frac{e^{iax}}{x^3+1}\,\mathrm{d}x-i\int_0^\infty\frac{e^{-ax}(1+ix^3)}{1+x^6}\,\mathrm{d}x\tag{2} \end{align} $$ Solving for the integral we want: $$ \begin{align} \int_0^\infty\frac{e^{iax}}{x^3+1}\,\mathrm{d}x &=-\int_0^\infty\frac{x^3e^{-ax}}{1+x^6}\,\mathrm{d}x-\frac{2\pi}3e^{-a\sqrt3/2}\sin\left(\frac a2-\frac{2\pi}3\right)\\ &+i\left[\int_0^\infty\frac{e^{-ax}}{1+x^6}\,\mathrm{d}x+\frac{2\pi}3e^{-a\sqrt3/2}\cos\left(\frac a2-\frac{2\pi}3\right)\right]\tag{3} \end{align} $$ Therefore, separating real and imaginary parts, we have $$ \int_0^\infty\frac{\cos(ax)}{x^3+1}\mathrm{d}x =-\int_0^\infty\frac{x^3e^{-ax}}{1+x^6}\,\mathrm{d}x-\frac{2\pi}3e^{-a\sqrt3/2}\sin\left(\frac a2-\frac{2\pi}3\right)\tag{4} $$ and $$ \int_0^\infty\frac{\sin(ax)}{x^3+1}\mathrm{d}x =\int_0^\infty\frac{e^{-ax}}{1+x^6}\,\mathrm{d}x+\frac{2\pi}3e^{-a\sqrt3/2}\cos\left(\frac a2-\frac{2\pi}3\right)\tag{5} $$

---

Asymptotic Expansion

Equations $(4)$ and $(5)$ show that as $a\to\infty$, the integrals vanish. In fact, it is not difficult to obtain an asymptotic expansion from the right hand side of these integrals: $$ \int_0^\infty\frac{x^3e^{-ax}}{1+x^6}\,\mathrm{d}x \sim\frac{3!}{a^4}-\frac{9!}{a^{10}}+\frac{15!}{a^{16}}-\dots\tag{6} $$ and $$ \int_0^\infty\frac{e^{-ax}}{1+x^6}\,\mathrm{d}x \sim\frac{0!}{a^1}-\frac{6!}{a^7}+\frac{12!}{a^{13}}-\dots\tag{7} $$ Unfortunately, neither Mathematica nor I have found any simpler formulas for these exponential integrals. However, Mathematica does verify that equations $(4)$ and $(5)$ hold numerically for several values of $a$.

---

Convergent Series

Although equations $(4)$ and $(5)$ are valid for any $a\ge0$ and make the integral easier to compute numerically, and $(6)$ and $(7)$ give good approximations for large $a$, the question has now been amended to express interest in small $a$.

Integration by parts gives $$ \newcommand{\Ein}{\operatorname{Ein}} \begin{align} \int_a^\infty\frac{e^{-x}}{x}\mathrm{d}x &=\int_0^a\frac{1-e^{-x}}{x}\mathrm{d}x-\log(a)-\gamma\\[6pt] &=\Ein(a)-\log(a)-\gamma\tag{8} \end{align} $$ where $$ \begin{align} \Ein(x)&=\sum_{k=1}^\infty(-1)^{k-1}\frac{x^k}{k\,k!}\tag{9}\\ \end{align} $$ or to remove oscillation for positive $x$: $$ \begin{align} e^x\Ein(x)&=\sum_{k=1}^\infty\frac{H_k}{k!}x^k\tag{10}\\ \end{align} $$ Therefore, $$ \begin{align} \int_0^\infty\frac{e^{-x}\mathrm{d}x}{x+a} &=e^a\int_a^\infty\frac{e^{-x}\mathrm{d}x}{x}\\[6pt] &=e^a\left(\Ein(a)-\log(a)-\gamma\right)\tag{11} \end{align} $$ A change of variables, partial fractions yields, and applications of $(10)$ and $(11)$ yield $$ \begin{align} &\int_0^\infty\frac{x^3e^{-ax}}{1+x^6}\,\mathrm{d}x\\ &=a^2\int_0^\infty\frac{x^3e^{-x}}{a^6+x^6}\,\mathrm{d}x\\ &=\small-\frac16\int_0^\infty\left(\frac1{x+ia}+\frac\omega{x+i\omega a}+\frac{\omega^2}{x+i\omega^2a}+\frac1{x-ia}+\frac\omega{x-i\omega a}+\frac{\omega^2}{x-i\omega^2a}\right)e^{-x}\,\mathrm{d}x\\ &=-\frac13\int_0^\infty\mathrm{Re}\left(\frac1{x+ia}+\frac\omega{x+i\omega a}+\frac{\omega^2}{x+i\omega^2a}\right)e^{-x}\,\mathrm{d}x\\ &=\sum_{k=0}^\infty(-1)^k\frac{H_{6k+2}}{(6k+2)!}a^{6k+2}\\ &+\small\frac13\left[\cos(a)-\cos\left(\tfrac12a\right)\cosh\left(\tfrac{\sqrt3}2a\right)-\sqrt3\sin\left(\tfrac12a\right)\sinh\left(\tfrac{\sqrt3}2a\right)\right](\log(a)+\gamma)\\ &+\frac\pi{18}\sin\left(\tfrac12a\right)\left[3\cosh\left(\tfrac{\sqrt3}2a\right)-2\sinh\left(\tfrac{\sqrt3}2a\right)\right]\\ &+\frac\pi{6\sqrt3}\cos\left(\tfrac12a\right)\left[2\cosh\left(\tfrac{\sqrt3}2a\right)-3\sinh\left(\tfrac{\sqrt3}2a\right)\right]\\ &-\frac\pi6\sin(a)\tag{12} \end{align} $$ and $(12)$ provides a real method to compute the integral appearing in $(4)$.

Similarly for the integral appearing in $(5)$ $$ \begin{align} &\int_0^\infty\frac{e^{-ax}}{1+x^6}\,\mathrm{d}x\\ &=a^5\int_0^\infty\frac{e^{-x}}{a^6+x^6}\,\mathrm{d}x\\ &=\small\frac16\int_0^\infty\left(\frac{i}{x+ia}+\frac{i\omega}{x+i\omega a}+\frac{i\omega^2}{x+i\omega^2a}-\frac{i}{x-ia}-\frac{i\omega}{x-i\omega a}-\frac{i\omega^2}{x-i\omega^2a}\right)e^{-x}\,\mathrm{d}x\\ &=-\frac13\int_0^\infty\mathrm{Im}\left(\frac1{x+ia}+\frac\omega{x+i\omega a}+\frac{\omega^2}{x+i\omega^2a}\right)e^{-x}\,\mathrm{d}x\\ &=\sum_{k=0}^\infty(-1)^{k+1}\frac{H_{6k+5}}{(6k+5)!}a^{6k+5}\\ &+\small\frac13\left[\sin(a)+\sin\left(\tfrac12a\right)\cosh\left(\tfrac{\sqrt3}2a\right)-\sqrt3\cos\left(\tfrac12a\right)\sinh\left(\tfrac{\sqrt3}2a\right)\right](\log(a)+\gamma)\\ &+\frac\pi{18}\cos\left(\tfrac12a\right)\left[3\cosh\left(\tfrac{\sqrt3}2a\right)-2\sinh\left(\tfrac{\sqrt3}2a\right)\right]\\ &-\frac\pi{6\sqrt3}\sin\left(\tfrac12a\right)\left[2\cosh\left(\tfrac{\sqrt3}2a\right)-3\sinh\left(\tfrac{\sqrt3}2a\right)\right]\\ &+\frac\pi6\cos(a)\tag{13} \end{align} $$

Answer 2

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\dsc}[1]{\displaystyle{\color{red}{#1}}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\Li}[1]{\,{\rm Li}_{#1}} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ \begin{align}&\color{#66f}{\large% \int_{0}^{\infty}{\cos\pars{ax} \over x^{3} + 1}\,\dd x} =a^{2}\int_{0}^{\infty}{\cos\pars{x} \over x^{3} + \verts{a}^{3}}\,\dd x =-\,{1 \over 3\verts{a}^{3}}\sum_{n\ =\ -1}^{1}x_{n}\int_{0}^{\infty} {\cos\pars{x} \over x - x_{n}}\,\dd x \\[5mm]&\mbox{where}\qquad x_{-1} \equiv \exp\pars{-\,{\pi\ic \over 3}}\verts{a}\,,\quad x_{0} \equiv -\verts{a}\,,\quad x_{1} \equiv \exp\pars{{\pi\ic \over 3}}\verts{a} \end{align}

Then, \begin{align}&\color{#66f}{\large% \int_{0}^{\infty}{\cos\pars{ax} \over x^{3} + 1}\,\dd x} ={1 \over 3a^{2}}\dsc{\int_{0}^{\infty}{\cos\pars{x} \over x + \verts{a}}\,\dd x} -{2 \over 3\verts{a}^{3}}\,\Re\bracks{x_{1}\dsc{\int_{0}^{\infty} {\cos\pars{x} \over x - x_{1}}\,\dd x}}\quad\pars{1} \end{align}

However, \begin{align}&\dsc{\int_{0}^{\infty}{\cos\pars{x} \over x + \mu}\,\dd x} =\int_{\mu}^{\infty}{\cos\pars{x - \mu} \over x}\,\dd x \\[5mm]&=\cos\pars{\mu}\int_{\mu}^{\infty}{\cos\pars{x} \over x}\,\dd x +\sin\pars{\mu}\int_{\mu}^{\infty}{\sin\pars{x} \over x}\,\dd x \\[5mm]&=-\cos\pars{\mu}\,{\rm Ci}\pars{\mu} +\sin\pars{\mu}\bracks{{\pi \over 2} - \,{\rm Si}\pars{\mu}} \\[5mm]&=\dsc{{\pi \over 2}\,\sin\pars{\mu} -\cos\pars{\mu}\,{\rm Ci}\pars{\mu} -\sin\pars{\mu}\,{\rm Si}\pars{\mu}}\tag{2} \end{align} where $\ds{\,{\rm Ci}}$ and $\ds{\,{\rm Si}}$ are the Cosine Integral and the Sine Integral , respectively.

In using the result $\pars{2}$, the integral $\pars{1}$ can be expressed in terms of the Cosine Integrals and Sine Integrals.