What's the point with neural networks if you can only predict linear test data?

Question

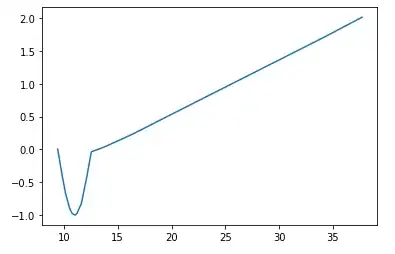
So, I have tried all the different activation functions listed on https://keras.io/api/layers/activations/. I can indeed approximate any nonlinear function in the training range perfectly well - but for any data outside the training range, I have a model that is limited to linear functions. For example, I tried to approximate the sinus function and had great results within the training range but was left with a linear function outside this range. I used a network with 3 hidden ReLU layers(with 16 units per layer) and an affine output layer. Here is the good approximation within the training range:

and the predictions outside the training range:

The same appends when trying to approximate any other nonlinear function. This is unfortunate because you would rather want your model to generalize well than to perform good exclusively on training data :( I could of course use a sine explicitly as an activation function but that seems to ridicule(maybe a strong word but you get the idea) the "self-learning" of neural networks.

This seems to make neural networks look very limited in my eyes - am I missing something?

I really appreciate your time!

Answer 1

Neural networks can generalize and successfully predict outside their training data. This ability is hindered by overfitting, where the network memorizes the training data and does not perform well on unseen data.

As with any other problem faced with neural networks, it is key for the network to have an inductive bias that is appropriate for the problem data. From this SO answer:

Every machine learning algorithm with any ability to generalize beyond the training data that it sees has some type of inductive bias, which are the assumptions made by the model to learn the target function and to generalize beyond training data.

For instance, convolutional networks perform well in image data due to their spatial locality inductive bias.

The main problem in your examples is that the function you are modeling is periodic while the activation functions you are using lack a periodic inductive bias. This problem is studied in the article Neural Networks Fail to Learn Periodic Functions and How to Fix It presented at NeurIPS 2020. From the abstract:

[...] we prove and demonstrate experimentally that the standard activations functions, such as ReLU, tanh, sigmoid, along with their variants, all fail to learn to extrapolate simple periodic functions. We hypothesize that this is due to their lack of a “periodic” inductive bias. As a fix of this problem, we propose a new activation, namely, $x + sin^2 (x)$, which achieves the desired periodic inductive bias to learn a periodic function while maintaining a favorable optimization property of the ReLU-based activations.

Answer 2

I’m a bit late, but there is something called a Fourier Analysis Network that is specifically designed to generalize for periodic functions: https://arxiv.org/abs/2410.02675

Answer 3

Disclaimer: my knowledge about neural networks is very limited, so my answer is only based on general ML principles. Hopefully somebody will provide a more informed answer.

In supervised learning, the assumption is that the training set is a representative sample of the data, i.e. a random subset of the whole sample space. From this point of view it's easy to explain why your model doesn't generalize the function outside the training range: the model expects only points in the same range as the training set. You and I know that the function is periodic over $\mathbb{R}$, but the model has no way to know that. For example the function could perfectly be "if x<20 then sin(x) else 0" with the same training data. So your conclusion is exaggerated: it's not that you can only predict linear data, but you need at least to provide a representative training sample.

I'm aware of at least two other interesting questions on the topic of the generalization ability of neural networks:

• Can a neural network compute y=x²?
• Can machine learning learn a function like finding maximum from a list?

Imho it's quite revealing that, based on the answers, the two questions appear to be quite controversial. It might also be of interest to note that in both questions there's an answer (here and there) which points out the theoretical limitation that the target function needs to be defined on a compact subset of $\mathbb{R}^n$.

Another vaguely related remark: a technique used with some [many? most? I don't know] forecasting problems is to explicitly train the model to predict the next point (or some point in the future) based on past data. By analogy, if the goal of the task is to predict points outside a particular range then the training data should be made of instances which represent a sequence of values so that the model can learn to predict the next point in a sequence. This design makes more sense with respect to providing a representative sample as training set. My guess is that a periodic function would be more likely to be correctly approximated in this way, but I didn't test the idea.