8

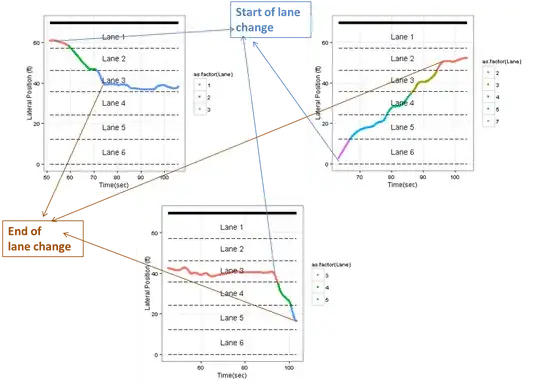
I have data for each vehicle's lateral position over time and lane number as shown in these 3 plots in the image and sample data below.

enter image description here

> a
   Frame.ID   xcoord Lane
1       452 27.39400    3
2       453 27.38331    3
3       454 27.42999    3
4       455 27.46512    3
5       456 27.49066    3

The lateral position varies over time because a human driver does not have perfect control over vehicle's position. The lane change maneuver starts when the lateral position changes drastically and ends when the variation becomes 'normal' again. This can not be identified from the data directly. I have to manually look at each vehicle's plot to determine the start and end points of lane change maneuver in order to estimate the duration of lane change. But I have thousands of vehicles in the data set. Could you please direct me to any relevant image analysis/ machine learning algorithm that could be trained to identify these points? I work in R. Thanks in advance.

umair durrani
  • 344
  • 1
  • 2
  • 8

3 Answers3

2

A first derivative, on the surface, would do it. However, the data you show have a great deal of noise in them, so we need a way to evaluate the first derivative in a somewhat noiseless way, or at least within a frequency domain that eliminates the jitter and preserves the major derivative change.

Wavelet analysis could achieve this for you, especially if you use the first derivative of a Gaussian as your mother wavelet. R has some decent wavelet packages (see r-project.org for starters). If you do the wavelet transform at short scales, this will identify the locations of the bits of jitter in the steering. If you do it at larger scales (i.e. lower frequency), you can likely find just the lane shifts and not the little jitters.

If you train the transform up with a reasonable data set, you should be able to identify a scale or range of scales that corresponds to lane changes. But note that if you don't figure that out, this is something like O(n^2), so try to narrow the scale range down a bit to save compute time.

CJ Sullivan
  • 121
  • 2
1

Looks like you could just look for a few seconds of higher then noise derivative. Just calculate the absolute value of the finite difference from each timestep to the last ( or one of the former ) and wait for a series of high values. That's when a lane change occurs.

Tobias Würfl
  • 101
  • 3
1

Try the changepoint package. I used it in a similar case.

Changepoint analysis is the statistical name for methods that detect changes between two "regimes". A car staying in a lane is a line with gradient 0 at the midpoint of a lane. You can easily fit a statistical model to cars driving in lanes. A car changing lane is driving along a line with a gradient that isn't 0. The model has changed. Changepoint analysis, and the changepoint package, is exactly what you need to determine the point when a model changes from y=a' (straight and level) toy=a+bx` (going up or down).

Spacedman
  • 2,042
  • 12
  • 17
AlbertoD
  • 27
  • 3