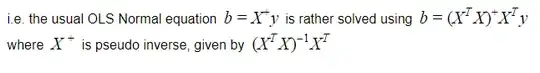Mathematical Details
1. Ordinary Least Squares (OLS):
OLS solves the problem of minimising the residual sum of squares:
$$
\hat{\beta} = \operatorname*{arg\,min}_{\beta} \| Y - X\beta \|^2
$$
where:
- $Y \in \mathbb{R}^n$ is the response vector,
- $X \in \mathbb{R}^{n \times p}$ is the design matrix,
- $\beta \in \mathbb{R}^p$ is the coefficient vector.
The closed-form solution is:
$$
\hat{\beta} = (X^T X)^{-1} X^T Y
$$
However, directly computing $(X^T X)^{-1}$ is often unstable for ill-conditioned matrices.
2. Moore-Penrose Pseudoinverse:
The Moore-Penrose pseudoinverse, $X^+$, is computed using the singular value decomposition (SVD):
$$
X = U \Sigma V^T, \quad X^+ = V \Sigma^+ U^T
$$
where:
- $U \in \mathbb{R}^{n \times n}$ and $V \in \mathbb{R}^{p \times p}$ are orthogonal matrices,
- $\Sigma \in \mathbb{R}^{n \times p}$ is diagonal with singular values,
- $\Sigma^+$ contains the reciprocal of non-zero singular values.
The solution is:
$$
\hat{\beta} = X^+ Y
$$
3. QR Decomposition:
QR decomposition expresses the design matrix as:
$$
X = Q R
$$
where:
- $Q \in \mathbb{R}^{n \times p}$ is orthogonal ($Q^T Q = I$),
- $R \in \mathbb{R}^{p \times p}$ is upper triangular.
The solution is obtained by solving $R\beta = Q^T Y$ via back-substitution.
Comparison
1. Numerical Stability
- Pseudoinverse (SVD): Handles rank-deficient matrices robustly by filtering out small singular values, making it suitable for ill-conditioned problems.
- QR Decomposition: Improves numerical stability by avoiding direct inversion of $X^T X$, though it is less robust than SVD in cases of rank deficiency.
2. Computational Efficiency
- Pseudoinverse (SVD): Computationally intensive with complexity $O(n p^2)$, suitable for small to moderate datasets.
- QR Decomposition: Also $O(n p^2)$ but faster in practice due to smaller constant factors, making it ideal for large datasets.
3. Practical Considerations
- Pseudoinverse: Preferred when the design matrix is rank-deficient or understanding singular values is critical.
- QR Decomposition: Favoured for standard overdetermined systems due to a better trade-off between speed and stability.
Summing Up
Both methods are effective for solving OLS regression problems, but their suitability depends on the problem context:
- Use the Moore-Penrose pseudoinverse for rank-deficient or ill-conditioned matrices.
- Opt for QR decomposition for large-scale regression problems requiring numerical efficiency.
References
- Golub, G. H., & Van Loan, C. F. (2013). Matrix Computations. Johns Hopkins University Press.
- Higham, N. J. (2002). Accuracy and Stability of Numerical Algorithms. SIAM.