I have a two-class prediction model; it has n configurable (numeric) parameters. The model can work pretty well if you tune those parameters properly, but the specific values for those parameters are hard to find. I used grid search for that (providing, say, m values for each parameter). This yields m ^ n times to learn, and it is very time-consuming even when run in parallel on a machine with 24 cores.
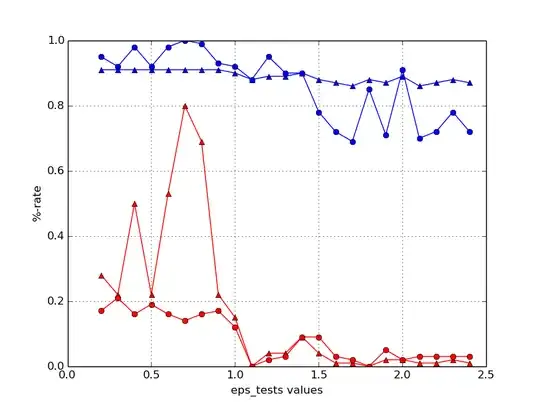
I tried fixing all parameters but one and changing this only one parameter (which yields m × n times), but it's not obvious for me what to do with the results I got. This is a sample plot of precision (triangles) and recall (dots) for negative (red) and positive (blue) samples:
Simply taking the "winner" values for each parameter obtained this way and combining them doesn't lead to best (or even good) prediction results. I thought about building regression on parameter sets with precision/recall as dependent variable, but I don't think that regression with more than 5 independent variables will be much faster than grid search scenario.
What would you propose to find good parameter values, but with reasonable estimation time?