Why are optimization algorithms slower at critical points?

Question

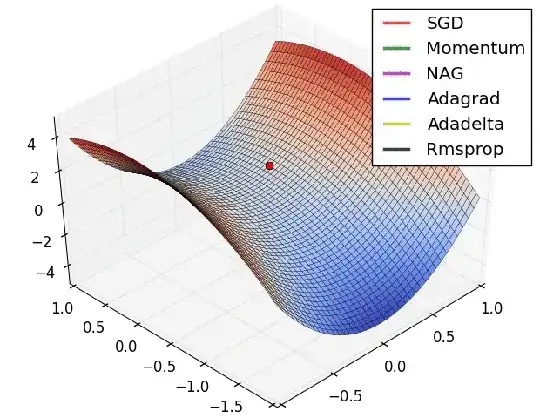
I just found the animation below from Alec Radford's presentation:

As visible, all algorithms are considerably slowed down at saddle point (where derivative is 0) and quicken up once they get out of it. Regular SGD itself is simply stuck at the saddle point.

Why is this happening? Isn't the "movement speed" constant value that is dependent on the learning rate?

For example, weight for each point on regular SGD algorithm would be:

$$w_{t+1}=w_t-v*\frac{\partial L}{\partial w}$$

where $v$ is a learning rate and $L$ is a loss function.

In short, why are all optimization algorithms slowed down by the saddle point even though step size is constant value? Shouldn't a movement speed be constantly same?

Answer 1

In that simulation, the movement speed is a proxy for step size. The step size is a function of learning rate (v) and the approximate gradient of the function at that point ($\frac{\partial L}{\partial w}$). The learning rate can be constant. However, the approximate gradient is not constant. The approximate gradient is typically smaller closer to a critical point (i.e., the valley starts to gradually level out). Thus, the computed update value is smaller and the movement speed slows down.