7

I've taken a few online courses in machine learning, and in general, the advice has been to choose random weights for a neural network to ensure that your neurons don't all learn the same thing, breaking symmetry.

However, there were other cases where I saw people initializing using zero weights. Unfortunately, I can't remember what those were. I think it might have been non-neural-network cases, like a simple linear or logistic regression model (simple weights only on the inputs, leading directly to an output).

Are those cases safe for zero initialization? Alternatively, could we use random initialization in those cases too, just to stay consistent?

Green Falcon
  • 14,308
  • 10
  • 59
  • 98
Stephen
  • 272
  • 2
  • 9

2 Answers2

9

Whenever you have a convex cost function you are allowed to initialize your weights to zeros. The cost function of logistic regression and linear regression have convex cost function if you use MSE for, also RSS, linear regression and cross-entropy for logistic regression. The main idea is that for convex cost function you'll have just a single optimal point and it does not matter where you start, the starting point just changes the number of epochs to reach to that optimal point whilst for neural networks the cost function does not have just one optimal point. Take a look at here. About random initialization, you have to consider that you are not allowed to choose random weights which are too small or too big although the former was a more significant problem. If you choose random small weights you may have vanishing gradient problem which may lead to a network that does not learn. Consequently, you have to use standard initialization methods like He or Glorot, take a look at here and Understanding the difficulty of training deep feedforward neural networks.

Also, take a look at the following question.

Green Falcon
  • 14,308
  • 10
  • 59
  • 98
2

Zeroing weights disables them. Yes, there are various applications of zero tensors (such as convex cost functions as you mention). Let's take the case of Neural Nets (NNs) and see if the math gives us more intuition:

$$ tensor\div0 = undefined\\ tensor * 0 = 0\\ tensor \cdot 0 = 0\\ $$

Example Graph #1: How would one disable a single synapse connected to the output layer?

                                                            

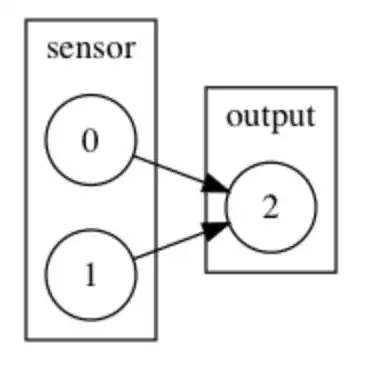
Math Example: Let $X$ be an input tensor of shape (1,2). Let $W$ be a weight tensor of shape (2,1). The dot product is represented here by the $\cdot$ symbol.

If all elements in tensor $W$ are zero:

$$ \begin{align*} X = \begin{matrix}[1&1]\\ \end{matrix}\ \ \ W = \begin{matrix}[0]\\ [0]\end{matrix}\ \end{align*} $$

$$ X \cdot W = [0]\\ $$

If all elements in tensor $W$ are randomly initialized (between -1 and 1):

$$ \begin{align*} X = \begin{matrix}[1&1]\\ \end{matrix}\ \ \ W = \begin{matrix}[0.24660266]\\ [0.05121049]\end{matrix}\ \end{align*} $$

$$ X \cdot W = [0.29781315]\\ $$

If one element in tensor $W$ is randomly set to zero:

$$ \begin{align*} X = \begin{matrix}[1&1]\\ \end{matrix}\ \ \ W = \begin{matrix}[0]\\ [0.05121049]\end{matrix}\ \end{align*} $$

$$ X \cdot W = [0.05121049]\\ $$

Aha, some intuition! Set an element of your weight vector $W$ to zero to disable it.

Example Graph #2: As complexity scales, so too does our potential loss of control over architecture.

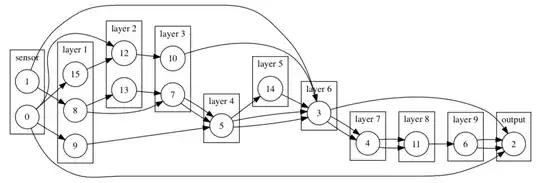
When you need to tweak the details, it is important to have tools to change nodes and edges on a per unit basis. Zero weighting gives you that ability.

This idea generalizes to CNNs, GANs, RNNs, etc. Look at the particular algorithm and go layer by layer. What are the designers trying to accomplish?

abrahamrhoffman
  • 31
  • 5