Let's say that I have two similar datasets with the same size of elements, for example 3D points :
And the question is that is there a way to measure the correlation/similarity／Distance between these two datasets ?
Any help will be appreciated.
I see a lot of people post this similar question on StackExchange, and the truth is that there is no methodology to compare if data set A looks like set B. You can compare summary statistics, such as means, deviations, min/max, but there's no magical formula to say that data set A looks like B, especially if they are varying data sets by rows and columns.
I work at one of the largest credit score/fraud analytics companies in the US. Our models utilize large number of variables. When my team gets a request for a report, we have to look at each individual variable to inspect that the variables are populated as they should be with respect to the context of the client. This is very time consuming, but necessary. Some tasks do not have magical formulas to get around inspecting and digging deep into the data. However, any good data analyst should understand this already.
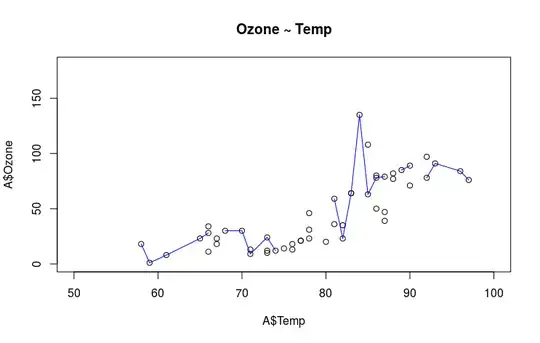
Given your situation, I believe you should identify key statistics of interest to your data/problems. You may also want to look at what distributions look like graphically, as well as how variables relate to others. If for data set A, Temp and Ozone are positively correlated, and if B is generated through the same source (or similar stochastic process), then B's Temp and Ozone should also exhibit a similar relationship.
My I will illustrate my point via this example:
data("airquality")
head(airquality)
dim(airquality)
set.seed(123)
indices <- sample(x = 1:153, size = 70, replace = FALSE) ## randomly select 70 obs
A = airquality[indices,]
B = airquality[-indices,]
summary(A$Temp) ## compare quantiles
summary(B$Temp)
plot(A)
plot(B)
plot(density(A$Temp), main = "Density of Temperature")
plot(density(B$Temp), main = "Density of Temperature")
plot(x = A$Temp, y = A$Ozone, type = "p", main = "Ozone ~ Temp",
xlim = c(50, 100), ylim = c(0, 180))
lines(lowess(x = A$Temp, y = A$Ozone), col = "blue")
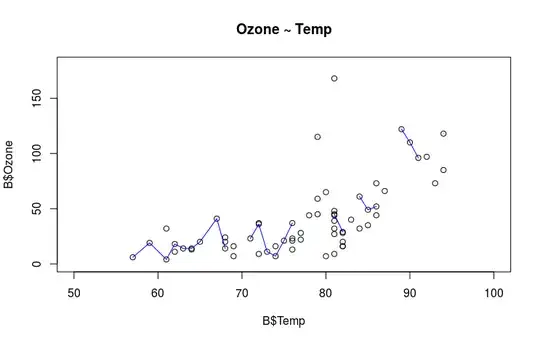
plot(x = B$Temp, y = B$Ozone, type = "p", main = "Ozone ~ Temp",
xlim = c(50, 100), ylim = c(0, 180))
lines(lowess(x = B$Temp, y = B$Ozone), col = "blue")
cor(x = A$Temp, y = A$Ozone, method = "spearman", use = "complete.obs") ## [1] 0.8285805
cor(x = B$Temp, y = B$Ozone, method = "spearman", use = "complete.obs") ## [1] 0.6924934
Well, if your samples are collections of points, I would separate this in two steps:
Calculate distances between inner points: choose how to calculate the distance between (1,2,3) and (2,1,3), for instance. Here, depending on the nature of your problem, you could go for something akin to the euclidean distance or if you only care about the orientation of the points, something like the cosine similarity.
Summarize all the distances as a single number: depending on your problem, you could get its average, its median or some other quantity. The main idea is to reduce all the numbers to a single one.
If you are interested in the 1-Dimensional distributions you could use a test (like a Kolmogorov-Smirnov test). I would naively expect that while this cant tell you if data is similar it can tell you if it is not. Or you create multidimensional histograms and calculate a Chi2 similar quantity. Obviously this can run into some problems if the parameter space is rather sparsely filled.
I would think your datasets as "Clusters" and there are some distance metrics for clusters.
https://stats.stackexchange.com/questions/270951/distance-between-2-clusters
