I posted this question on Cross Validated before I realized that this existed. I think it is better suited here and got no answers over there so I have deleted other post. I have reproduced the question below:
I have been playing around with the neural network toolbox in MATLAB to develop an intuition for how the architectural requirements scale with feature dimension.
I put together a simple example, and the results have surprised me. I am hoping someone can point to either (a) an unrealistic expectation of mine, or (b) a mistake/misuse of the neural network toolbox.
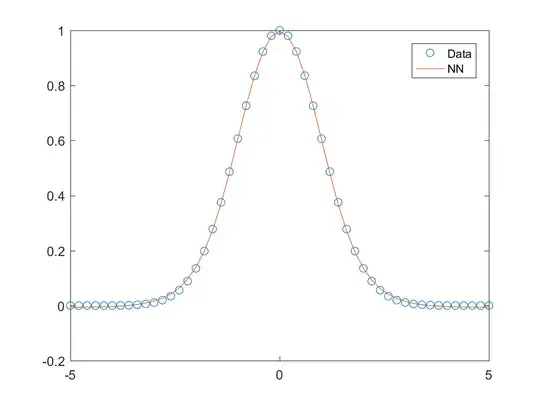
The example is as follows: I have a simple un-normalized one-dimensional Gaussian that I am trying to learn. I do the following:
x = -5:0.2:5;
y = exp(-x.^2/2);
net = feedforwardnet(2);
net = configure(net, x, y);
net = train(net, x, y);
y2 = net(x);
plot(x, y, 'o', x, y2);
legend('Data', 'NN');
This gives me good results. I get the plot below.
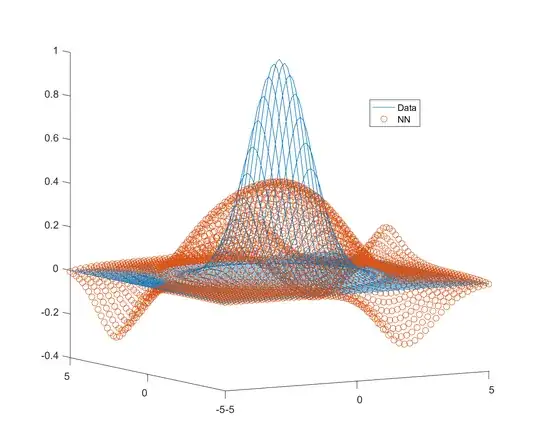
Now, I try to extend this to 2 dimensions and this is where I run into trouble. I don't think I'm asking too much. My data is not noisy, or is it sparse. I figure if I double the number of neurons that should be sufficient for an increase in dimensionality. Here's my code:
x1 = -5:0.2:5;
x2 = -5:0.2:5;
[x1g, x2g] = meshgrid(x1, x2);
xv = [x1g(:)'; x2g(:)'];
yv = exp(-dot(xv,xv)/2);
net = feedforwardnet(4);
net = configure(net, xv, yv);
net = train(net, xv, yv);
y2v = net(xv);
plot3(xv(1,:), xv(2,:), yv, xv(1,:), xv(2,:), y2v, 'o');
legend('Data', 'NN');
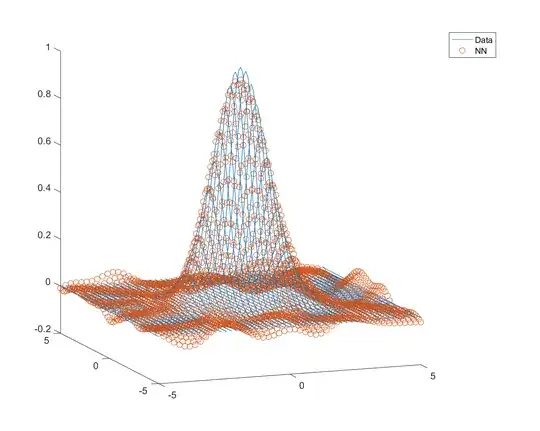
The plot I get is this:
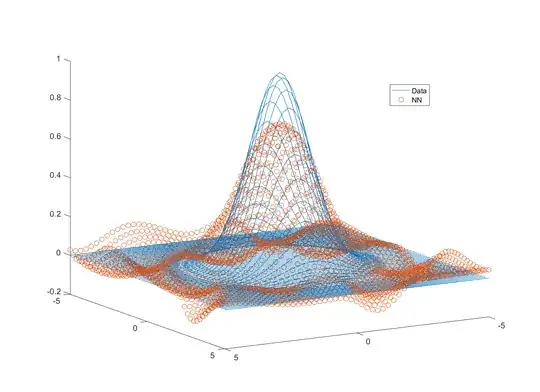
This is pretty poor. Perhaps I need more neurons? Maybe if I double the number of dimensions, I need to quadruple the number of neurons. I get this for 8 neurons:
Maybe with 8 neurons I have a lot of weights to fit, so let me try training with regularization. I get the plot below with trainbr:
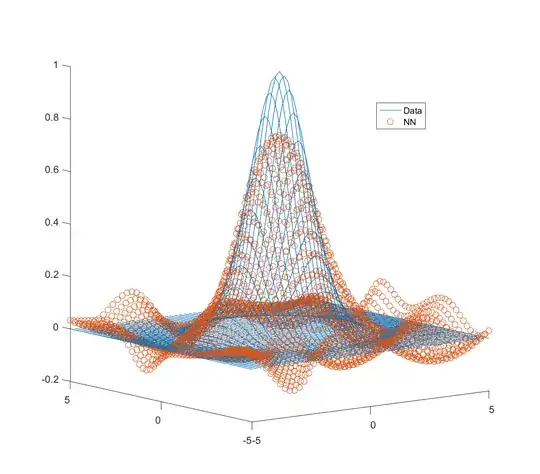
It's only at around 16 neurons that I start getting something I would consider reasonable.
However, there are still oscillations which I don't like. Now I know I'm using it out of the box in a naïve manner, or perhaps I'm expecting too much. But this simple example resembles the real problem I want to tackle. I have the following questions:
- Why is it that an increase from 1 to 2 dimensions increases the number of neurons required to get a decent fit considerably?
- Even when I go to a larger number of neurons, I get oscillations that are going to be a problem in my real world application. How can I get rid of that?
- Most resources on NN that I've read indicate a substantially lower number of neurons. They usually state something like "equal to or less than the number of input variables". Why is that? Is a multidimensional Gaussian a pathological case?
- If I need to be more intelligent with how I treat my network for a given number of neurons, what do I need to do? I tried retraining the network to see if it was a local minima issue, but I generally get a similar fit.
- Anything else that may be remotely useful to this issue is appreciated!