I know that for hierarchical clustering, it's the best practice to scale before so that you give the same weight to each variable. Otherwise, for the complete linkage, the variable with a wider range would be a dominant factor when determining which clusters to combine.
My question is, for the single linkage without scaling, is the variable with a wider range would be a dominant factor when determining which clusters to combine as the complete linkage? thanks in advance
Yes, a wider-range-variable would dominate the single linkage clustering without scaling.
The tendency of wider-range-variables to dominate the clustering does not only apply to hierachical clustering, but to many clustering methods.
The reason for this lies below the clustering: most (if not every) clustering algorithm is based on a distance metric. If not otherwise specified, the euclidean distance is typically uses. And this metric is dominated by the wide-range variables. Hence, the clustering algorithms that rely on such a metric, are as well dominated by the wider-range-variables.
Normalizing is the easiest way to handle this problem (if it is a problem). Using different metrics would be another way. E.g. the Mahalanobis distance does kind of a normalization by it self. Another approach would be a custom metric that uses some domain knowledge.
Do demonstate this, I created a example dataset with
And clustered it with
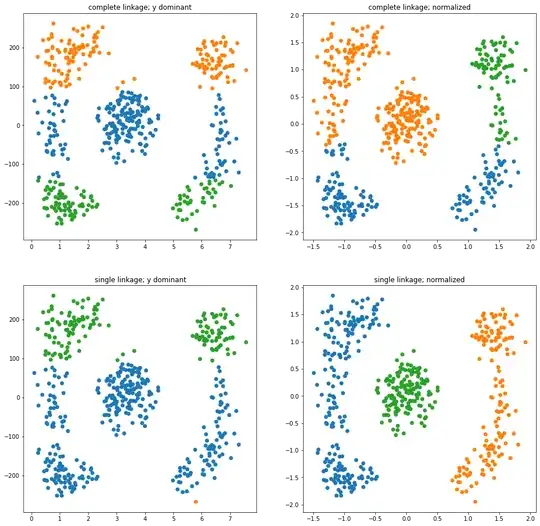
As you can see, the non-normalized data (left column) is clustered nearly exclusivly by the y-value.
You also see that the complete linkage prefers compact clusters (top row, both columns), while the single linkage avoids bigger gaps (bottom row, right image)