1

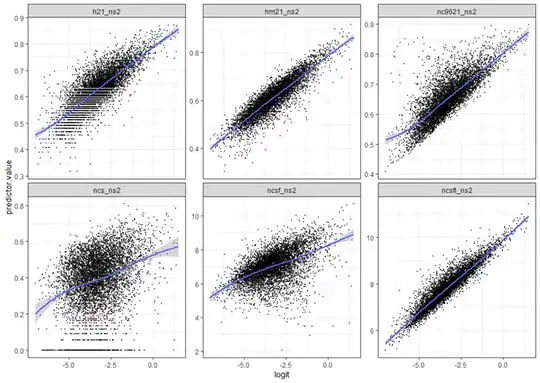
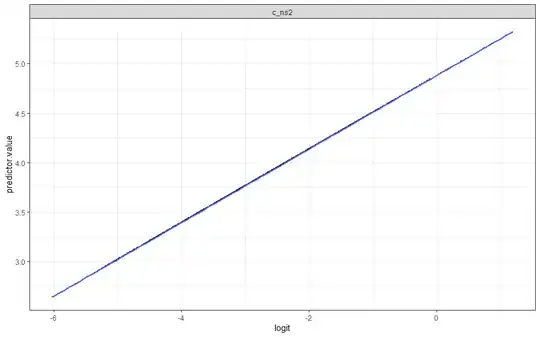
Question: Why is my predictor value (continuous) perfectly correlated with my logit value (when testing logistic regression model assumptions)?

Code:

# linearity in the logit for continuous var: check the linear relationship bw continuous predictor var and the logit of the outcome: inspect scatter plot bw each predictor and logit value
# Select only continuous predictors
glm_h2_a1 <- df_master_aus %>%
  dplyr::select(c(c_ns2)) 
predictors <- colnames(df_master_aus)
# bind the logit and tidying the data for plot
glm_h2_a1 <- glm_h2_a1 %>%
  mutate(logit = log(probabilities/(1-probabilities))) %>%
  gather(key = "predictors", value = "predictor.value", -logit)

create the Scatter Plots:


ggplot(glm_h2_a1, aes(logit, predictor.value))+
  geom_point(size = 0.5, alpha = 0.5) +
  geom_smooth(method = "loess") + 
  theme_bw() + 
  facet_wrap(~predictors, scales = "free_y")

Image: enter image description here

Note: More complex model with additional predictors do not all show such linearity: enter image description here

In_cognito
  • 11
  • 2

1 Answers1

0

$$ \text{logit}=\hat\beta_0+\hat\beta_1x\\ \text{cor}(x, \text{logit})\\ =\text{cor}(x, \hat\beta_0+\hat\beta_1x)\\ =\text{cor}(x, \hat\beta_1x) $$

If the estimated slope coefficient $\hat\beta_1>0$, then $\text{cor}(x,\hat\beta_1x)=\text{cor}(x,x)=1$.

Consequently, this does not test any assumptions: by definition, the linear prediction of your logistic regression model has a perfect (perhaps negative) correlation with the feature. If you understand why the feature in a simple linear regression is perfectly correlated (perhaps negatively) with the predictions, the same idea applies here.

Dave
  • 4,542
  • 1
  • 10
  • 35