I have some time series, like this one:
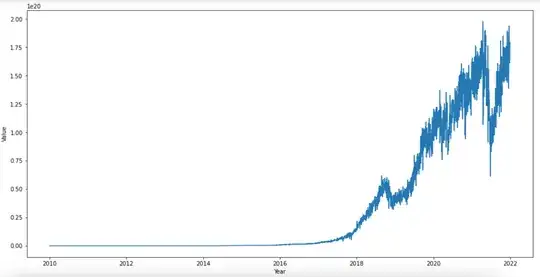 I want to predict future values, so I splitted in train/test (70/30) and I created several ARIMA models, however they are all completely wrong (or maybe I am wrong).
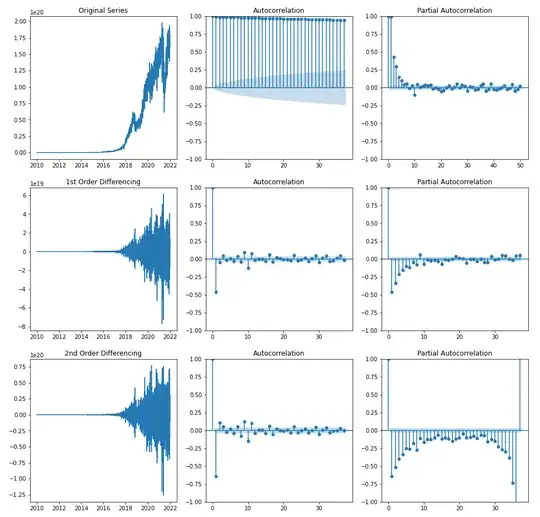
First of all, considering differentiation, ACF and PACF, I supposed that a good model can be an ARIMA(2,2,2) or something similar (spoiler: I did not found any good model)
I want to predict future values, so I splitted in train/test (70/30) and I created several ARIMA models, however they are all completely wrong (or maybe I am wrong).
First of all, considering differentiation, ACF and PACF, I supposed that a good model can be an ARIMA(2,2,2) or something similar (spoiler: I did not found any good model)
 I transformed the data with a box-cox transformation, in order to have more similar values, so from
I transformed the data with a box-cox transformation, in order to have more similar values, so from
Timestamp Value year month
Timestamp
2010-01-01 2010-01-01 5.948447e+06 2010 Jan
2010-01-01 2010-01-01 1.116364e+07 2010 Jan
2010-01-02 2010-01-02 5.272979e+06 2010 Jan
2010-01-02 2010-01-02 1.015796e+07 2010 Jan
2010-01-03 2010-01-03 1.091864e+07 2010 Jan
to
Timestamp Value year month
Timestamp
2010-01-01 2010-01-01 29.411458 2010 Jan
2010-01-01 2010-01-01 31.462963 2010 Jan
2010-01-02 2010-01-02 29.029479 2010 Jan
2010-01-02 2010-01-02 31.149175 2010 Jan
2010-01-03 2010-01-03 31.389007 2010 Jan
As input target variable I stated "Value". Then, I found this nice function that allows to create SARIMAX models:
def model_auto_sarimax(y, seasonality, seasonal_flag, exogenous_variable):
# Train model
model = pm.auto_arima(train[input_target_variable], exogenous=exogenous_variable,
start_p = 1, start_q = 1,
max_p = 3, max_q = 3, m = input_seasonality,
start_P = 0, seasonal = seasonal_flag,
d = None, max_D = 1, trace = True,
error_action ='ignore',
suppress_warnings = True, stepwise = True,
max_order=12)
# Model summary
print(model.summary())
# Model diagnostics
model.plot_diagnostics(figsize=(10,7))
plt.show()
return model
And finally, this function to get predictions:
def get_predictions(input_ts_algo, model, train, test, input_target_variable, exogenous_variable = None):
print("------------- Get Predictions --------------- \n")
# Get prediction for test duration
if input_ts_algo == "manual_sarima":
predictions = pd.Series(model.predict(len(train) + 1, len(train) + len(test), typ = 'levels').rename("Predictions")).reset_index(drop = True)
elif input_ts_algo in ["auto_arima", "auto_sarima", "auto_sarimax"]:
predictions = pd.Series(model.predict(len(test), exogenous = exogenous_variable)).reset_index(drop = True)
else:
predictions = pd.Series(model.forecast(len(test))).reset_index(drop = True)
return predictions
Now, considering a SARIMA model I call the previous declared functions (and some others)
print("------------- Auto SARIMA --------------- \n")
model = model_auto_sarimax(y = train[input_target_variable], seasonality = 7, seasonal_flag = True, exogenous_variable = None)
predictions = get_predictions(input_ts_algo, model, train, test, input_target_variable, exogenous_variable = None)
evaluate_model(actuals, predictions)
(Please note that seasonality=7 is only an attempt, because I tried with lot of values, but I am not sure of which using, this is only an example). These are some results:
------------- Auto SARIMA ---------------
Performing stepwise search to minimize aic
ARIMA(1,1,1)(0,0,1)[7] intercept : AIC=12761.725, Time=0.92 sec
ARIMA(0,1,0)(0,0,0)[7] intercept : AIC=14108.718, Time=0.06 sec
ARIMA(1,1,0)(1,0,0)[7] intercept : AIC=13227.472, Time=0.45 sec
ARIMA(0,1,1)(0,0,1)[7] intercept : AIC=12759.944, Time=0.69 sec
ARIMA(0,1,0)(0,0,0)[7] : AIC=14113.178, Time=0.06 sec
ARIMA(0,1,1)(0,0,0)[7] intercept : AIC=12757.961, Time=0.31 sec
ARIMA(0,1,1)(1,0,0)[7] intercept : AIC=12759.942, Time=0.56 sec
ARIMA(0,1,1)(1,0,1)[7] intercept : AIC=12760.164, Time=1.77 sec
ARIMA(1,1,1)(0,0,0)[7] intercept : AIC=12759.758, Time=0.45 sec
ARIMA(0,1,2)(0,0,0)[7] intercept : AIC=12759.784, Time=0.53 sec
ARIMA(1,1,0)(0,0,0)[7] intercept : AIC=13226.206, Time=0.16 sec
ARIMA(1,1,2)(0,0,0)[7] intercept : AIC=12759.991, Time=1.36 sec
ARIMA(0,1,1)(0,0,0)[7] : AIC=12869.046, Time=0.10 sec
Best model: ARIMA(0,1,1)(0,0,0)[7] intercept
------------- Get Predictions ---------------
------------- Model Evaluations ---------------
MAPE : 10.758296890064576
MAE : 43.21650273949536
RMSE : 51.58017099571381
R2 Score : -10.690625135150933
Durbin Watson Score : 0.005276384675653324
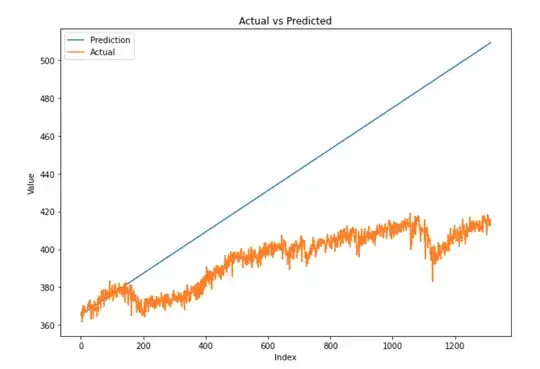 As you can see predictions are completely different. Model is predicting a straight line. Obviously also after anti-transforming the values after normalization:
As you can see predictions are completely different. Model is predicting a straight line. Obviously also after anti-transforming the values after normalization:
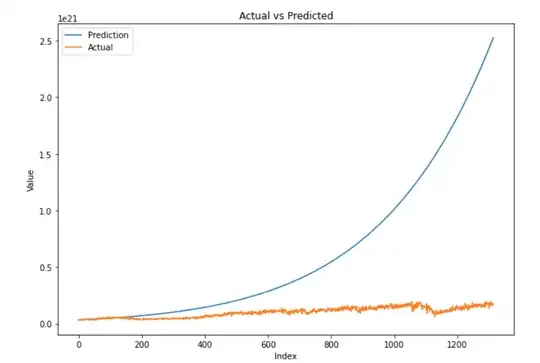 So, I am very confused. I do not know all these models are so poor. I tried all possible configurations, changing models, seasonality and so on. Moreover, I tried also with a smaller series, removing data before 2018 because they are very small, but also in this case I have bad results.
My question is: there is something strange in the code, or I am wrong with the models and parameters?
So, I am very confused. I do not know all these models are so poor. I tried all possible configurations, changing models, seasonality and so on. Moreover, I tried also with a smaller series, removing data before 2018 because they are very small, but also in this case I have bad results.
My question is: there is something strange in the code, or I am wrong with the models and parameters?
EDIT: This is how I import my data
hash_rate = pd.read_csv("data/bitcoin-mean-hash-rate.csv")
hash_rate["Hash Rate/t"] = hash_rate["Hash Rate/t"].str.rstrip("T00:00:00.000Z")
hash_rate["Hash Rate/t"] = pd.to_datetime(hash_rate["Hash Rate/t"])
hash_rate = hash_rate.sort_values(by='Hash Rate/t')
hash_rate = hash_rate.rename(columns={'Hash Rate/t': 'Timestamp', 'Hash Rate/v': 'Value'})
################ REMOVING BEFORE 2009 E 2022
hash_rate = hash_rate[~(hash_rate['Timestamp'] < '2010-01-01')]
hash_rate = hash_rate[~(hash_rate['Timestamp'] > '2021-12-31')]
#fixing index
hash_rate.index = hash_rate['Timestamp']
And here is the link to download data: Data
EDIT: Most of you are suggesting that the wrong part is that I am doing prediction for a too long time, and that the predictions can be correct for a small period of time. So, here is the prediction using 99% as training set and 1% as test set, so less than 50 days. As you can see is still a straight line.
 Moreover, some of you are saying that (S)ARIMA models are not able to fit data with 2 observations per day, while some others say that (S)ARIMA can. So now I am confused... however I am going to try also after a resampling. However, in my opinion the wrong part is in the prediction.
Moreover, some of you are saying that (S)ARIMA models are not able to fit data with 2 observations per day, while some others say that (S)ARIMA can. So now I am confused... however I am going to try also after a resampling. However, in my opinion the wrong part is in the prediction.
EDIT: I can confirm that the prediction part is the wrong one. Indeed, I have used the code of another notebook I found online, and here are the results:
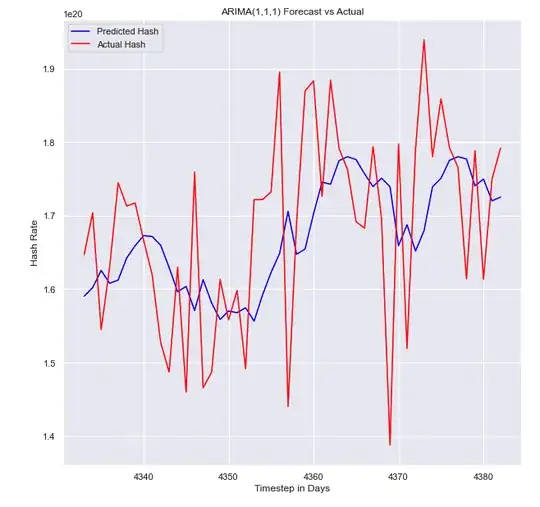 This is the new function used for fitting and prediction. You can compare with the previous one:
This is the new function used for fitting and prediction. You can compare with the previous one:
# Create list of x train valuess
history = [x for x in x_train]
establish list for predictions
model_predictions = []
Count number of test data points
N_test_observations = len(x_test)
loop through every data point
for time_point in list(x_test.index[-185:]):
model = sm.tsa.arima.ARIMA(history, order=(1,1,1))
model_fit = model.fit()
output = model_fit.forecast()
yhat = output[0]
model_predictions.append(yhat)
true_test_value = x_test[time_point]
history.append(true_test_value)
MAE_error = mean_absolute_error(x_test, model_predictions)
print('Testing Mean Squared Error is {}'.format(MAE_error))