Computer Science Stack Exchange
Computer Science Stack Exchange

Questions tagged [nearest-neighbour]

The point from the dataset that is closest to the query point.

Questions related to Nearest Neighbour Search (NNS) should have this tag. Questions on data structures (KD-trees for example) that aim to NNS should have this tag.

Given a set P in R^D, and a query point q, it's Nearest Neighbour (NN) is point p_0 in P, where:

dist(p_0, q) <= dist(p, q), for every p in P.

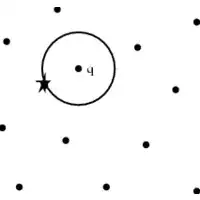
In the image below, the dots are the points of the dataset. q is the query point. The marked point (with a star) is the closest point to q, thus it's the NN.

enter image description here

For more: k-NN algorithm - wikipedia

79 questions
10
votes
1 answer

Why Is KD-Tree-based Nearest Neighbor Exponential in K?

I've read in many papers on higher-dimensional nearest neighbor search that KD-Trees are exponential in K, but I can't seem to determine why. What I'm looking for is a solid runtime-complexity analysis which explains this aspect of the problem.
akdom
  • 200
  • 5
8
votes
2 answers

How to efficiently compute the most isolated point?

Given a finite set $S$ of points in $\mathbb R^d$, how can we efficiently compute a "most isolated point" $x\in S$? We define a "most isolated point" $x$ by $$x = \arg\max_{p \in S} \min_{q \in S \setminus \{p\}} d(p,q)$$ (I used the $x=\arg\min$…
flawr
  • 373
  • 1
  • 10
7
votes
2 answers

A key-value datastructure with fast (on average) member move and nearest neighbors search?

I have a 3 dimensional float key search space (say a simulation world). I want to keep my values (ints, agent ids) in a data structure that can perform nearest neighbors search (with search for N neighbors in a range surrounding a given key) as fast…
DuckQueen
  • 201
  • 1
  • 2
7
votes
3 answers

Find k nearest neighbors on a sphere

Given a set $S$ of $N$ points on a sphere, and another point $P$ on the sphere, I want to find the $k$ points in $S$ that are the closest (Euclidean or great circle distance). I'm willing to do a reasonable amount of pre-computation. The solution…
JohnJ
  • 173
  • 1
  • 5
7
votes
2 answers

Fast and space efficient data structure for nearest neighbors in 3 dimensions?

I am looking for data structures to answer nearest neighbor queries in 3D which are reasonably space efficient (ie use at most $O(n^{1+\epsilon})$ space) and fast ($O(n^{\epsilon})$ or $O(log^k(n))$ query time in the worst case). As a summary of…
Mikola
  • 171
  • 4
6
votes
2 answers

Finding k-nearest neighbors to a set of nodes in a large graph

Given a large graph $G=(V,E)$, a set of nodes $S\subseteq V$, the problem is finding the $k$-nearest nodes in $V$ to the nodes in $S$. Given a pair of nodes $(u,v)$, the distance $d(u,v)$ between $u$ and $v$ is defined as the length of the shortest…
mhn_namak
  • 227
  • 2
  • 9
6
votes
1 answer

Find the closest string to a fixed set of strings

I want to find the closest string to a fixed set of strings. The strings are all equal in length, and the number of strings in the set is relatively small (compared to all the possible strings of the fixed size). For this problem you can assume the…
spyr03
  • 238
  • 1
  • 8
5
votes
1 answer

n closest points in a set of lat/long coordinates

Here's my problem: I have a website where people can search based on their location (which is converted to lat/long coordinates). I have many products stored in a database with their lat/long coordinates. I also have a function to calculate the…
Wouter Florijn
  • 215
  • 1
  • 6
5
votes
2 answers

How do I choose an optimal cell size when searching for close pairs of points, and using cells to implement this?

Suppose that I have a set of $N$ points in $k$-dimensional space ($k>1$), such as in this question, and that I need to find all pairs with a distance¹ smaller than a certain threshold $t$. The brute-force method would require $N(N-1)$ distance…
gerrit
  • 155
  • 8
4
votes
0 answers

Repeated nearest-neighbor queries

If I want to make N repeated (i.e. millions of) 2D nearest-neighbor queries on a pointset of size M, is traveling down into a KD-Tree most efficient or are there better ways to do this? (e.g. Voronoi?) Right now I'm building a KD-Tree of size M, so…
i_am_goose
  • 141
  • 2
4
votes
1 answer

Finding pairs of points that have a given offset

Problem: Given a set of points $S = \{x_1, x_2, x_3, ..., x_n\}$ from $\mathbb{R}^m$ and an offset vector $v \in \mathbb{R}^m$, find a set $Z \subseteq S \times S$ containing $k$ pairs of points $(x_i, x_j)$ such that the quantity $|x_i-x_j-v|$…
Alexandre
  • 349
  • 2
  • 10
4
votes
2 answers

Is the Nearest Neighbor Algorithm a valid algorithm to find a Minimum Spanning Tree?

I just wrote a program that runs the Travelling Salesman Problem using the Nearest Neighbor Algorithm. Afterwards, I started looking into Minimum Spanning Trees (MST). From my understanding: The Nearest Neighbor Algorithm traverses a graph starting…
JustBlossom
  • 245
  • 1
  • 3
  • 8
4
votes
1 answer

Best data structure for high dimensional nearest neighbor search

I'm actually working on high dimensional data (~50.000-100.000 features) and nearest neighbors search must be performed on it. I know that KD-Trees has poor performance as dimensions grows, and also I've read that in general, all space-partitioning…
mavillan
  • 141
  • 3
4
votes
3 answers

Nearest line-segment to a query point or conversely

I have a set of line segments (say 1000 of them) and a query point. I want to find the segment which is the closest in the Euclidean sense (if the point does not project on the segment I accept two options: 1) just ignore the segment - infinite…
user16034
4
votes
0 answers

Is there a name for the class of distance functions that are compatible with k-d trees?

The typical nearest neighbor search implementation for k-d trees prunes branches when the distance between the target and the pivot along the current axis exceeds the smallest distance found so far. This is correct (doesn't wrongly prune any…
Tavian Barnes
  • 105
  • 9
1
2 3 4 5 6