Knight and knaves

Question

I have these in my lecture notes, its about the rules where knights always tell the truth and knaves always lie:

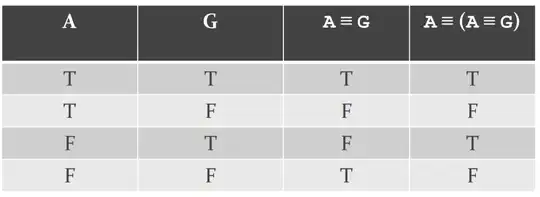
If A says “The statement ‘there is gold on the island’ and the statement ‘I am a knight’ are either both true or both false” he is asserting A ≡ G where A is the assertion A is a knight and G the assertion there is gold on the Island. Any assertion by a native has the same truth value as A so: A ≡ (A ≡ G)

(A ≡ A) ≡ G

true ≡ G

Since A ≡ (A ≡ G), it can only be the first case or third case. Hence, G is true and A can be true or false

The notes end here, I just don't understand why is it not possible for A to lie about being a knight and about gold being on the island, I mean it just shows that A is a knave, it should still be legal, even though the truth table says its illegal for the that to happen(last row), I just can't internalize why.

Answer 1

I suspect your confusion is about the different statuses of the following two things:

1. the single statement "I am a knight and there is gold";
2. the two statements "I am a knight" and "there is gold".

The question is talking about the second situation. In this case, the speaker is either a knight (in which case both statements are true) or a knave (in which case both are false: he is not a knight and there is no gold).

In the first case, if the speaker is a knight, then the statement is true, which means that both halves are true: he is a knight and there is gold. If the speaker is a knave, then the statement is false, but that only means that one or more of the halves are false. Surely the speaker is not a knight, and that fact is enough to make the "and" false on its own. But the second half of the statement could be true or false and the conjunction would still be false. So we don't know if there's gold or not.

But the question talks about case 2: there are two separate statements, not a single statement with "and" in the middle. It's the difference between $\neg A\land \neg B$ and $\neg (A\land B)$.