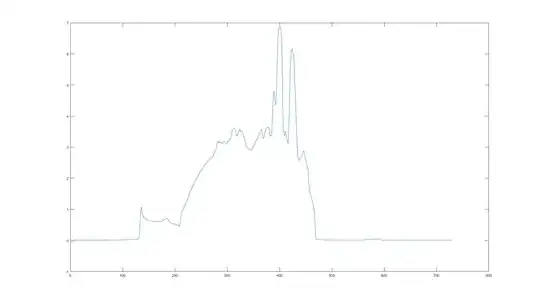
I have some signals that look like following:
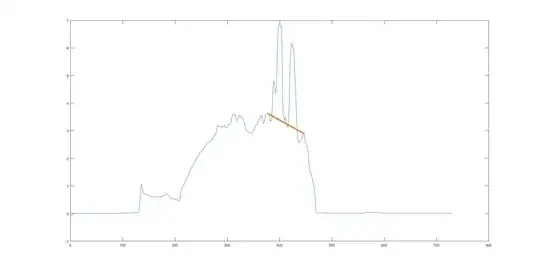
I would like to remove the two peaks by doing linear interpolation, so I can get something like this:
 where the orange line segment should replace the two peaks after the interpolation.
where the orange line segment should replace the two peaks after the interpolation.
I understand this very difficult because even for human being you can do it differently like this:

So it is really a challenging problem, and might not be a definite answer, but I just think something that looks comfortable, natural, and capturing details as much as possible.
I tried using mask, but edge is pretty noisy, and often times the width of the mask is far from the actual width of the spike. I also tried smoothing, and then applying finite difference to detect the starting and end position of the edges, but again it really does not as accurate as it should be.
I am wondering anyone has experience dealing with this problem? What algorithm I should use? Any literature describing the processing?
For this particular example, the data is here:
-0.0568
-0.0536
-0.0528
-0.0500
-0.0379
-0.0169
-0.0005
0.0127
0.0075
0.0133
0.0123
0.0130
0.0084
0.0126
0.0144
0.0030
0.0093
0.0168
0.0101
0.0096
0.0078
0.0117
0.0106
0.0138
0.0128
0.0059
0.0075
0.0062
0.0056
0.0017
0.0037
0.0173
0.0114
0.0143
0.0113
0.0117
0.0040
0.0118
0.0085
0.0079
0.0063
0.0152
0.0064
0.0024
0.0058
0.0041
0.0101
0.0086
0.0086
0.0154
0.0018
0.0130
0.0094
0.0094
0.0096
0.0103
0.0170
0.0081
0.0035
0.0138
0.0123
0.0031
0.0120
0.0039
0.0043
0.0063
0.0191
0.0023
0.0165
0.0174
0.0129
0.0135
0.0153
0.0100
0.0066
0.0135
0.0109
0.0038
0.0129
0.0084
0.0095
0.0109
0.0121
0.0077
0.0116
0.0128
0.0101
0.0158
0.0134
0.0042
0.0054
0.0063
0.0059
0.0136
0.0029
0.0139
0.0104
0.0215
0.0180
0.0153
0.0187
0.0138
0.0236
0.0190
0.0267
0.0209
0.0112
0.0108
0.0238
0.0280
0.0266
0.0300
0.0256
0.0278
0.0260
0.0263
0.0257
0.0334
0.0309
0.0301
0.0325
0.0280
0.0300
0.0286
0.0359
0.0317
0.0381
0.0348
0.0422
0.0389
0.0491
0.1754
0.4760
0.8146
1.0172
1.0757
0.9471
0.8509
0.7955
0.7526
0.7314
0.7092
0.7073
0.6906
0.6787
0.6654
0.6646
0.6553
0.6420
0.6385
0.6390
0.6373
0.6305
0.6216
0.6218
0.6212
0.6108
0.6161
0.6054
0.6106
0.6006
0.6032
0.6100
0.6006
0.5975
0.6042
0.6027
0.6044
0.6138
0.6106
0.6051
0.6084
0.6065
0.6212
0.6207
0.6306
0.6270
0.6484
0.6605
0.6742
0.6828
0.6972
0.7076
0.7062
0.6918
0.6905
0.6759
0.6459
0.6134
0.5989
0.5790
0.5663
0.5595
0.5609
0.5467
0.5442
0.5400
0.5317
0.5267
0.5182
0.5187
0.5101
0.4975
0.4951
0.4907
0.4855
0.4745
0.4505
0.4604
0.5814
0.7370
0.8355
0.9012
0.9498
0.9783
1.0188
1.0496
1.0727
1.1201
1.1639
1.2085
1.2465
1.2691
1.3170
1.3553
1.4211
1.4715
1.5169
1.5694
1.5963
1.6341
1.6722
1.7125
1.7388
1.7725
1.8040
1.8505
1.8817
1.9064
1.9337
1.9837
1.9992
2.0385
2.0719
2.1062
2.1415
2.1767
2.2151
2.2385
2.2427
2.2591
2.2856
2.3185
2.3572
2.3638
2.3905
2.4077
2.4429
2.4662
2.4841
2.4977
2.5204
2.5549
2.5709
2.5810
2.6063
2.6301
2.6245
2.6519
2.6594
2.6707
2.6836
2.7045
2.7642
2.8208
2.8278
2.8821
2.8950
2.9526
3.0908
3.1539
3.1935
3.1544
3.1317
3.1717
3.1677
3.1526
3.1489
3.1292
3.1129
3.1293
3.1561
3.1556
3.1857
3.1856
3.1327
3.1160
3.0868
3.1122
3.1407
3.1970
3.2136
3.2211
3.2376
3.2222
3.2521
3.3035
3.4006
3.5001
3.5602
3.5756
3.6020
3.6014
3.5830
3.5640
3.5016
3.4363
3.3618
3.3640
3.4059
3.4812
3.4943
3.5307
3.5735
3.5193
3.5079
3.5052
3.4986
3.4955
3.4303
3.3649
3.3260
3.2755
3.1902
3.0984
3.0574
3.0174
2.9852
2.9648
2.9462
2.9398
2.9393
2.9490
2.9268
2.9042
2.9143
2.9065
2.9340
3.0154
3.0141
3.0202
3.0782
3.1301
3.1803
3.2108
3.2176
3.2588
3.2822
3.3173
3.3732
3.3976
3.4492
3.4675
3.5090
3.5702
3.5230
3.4513
3.3371
3.2674
3.2867
3.3829
3.4563
3.5314
3.5805
3.6043
3.6157
3.6267
3.6450
3.6317
3.5860
3.4163
3.3502
3.3793
3.3572
3.5124
3.8337
4.2717
4.6394
4.8060
4.7245
4.5504
4.3687
4.3737
4.6887
5.4021
6.0749
6.5674
6.7279
6.8391
6.8456
6.8219
6.8410
6.7609
6.5246
5.7718
4.4415
3.5784
3.4720
3.3728
3.4125
3.5051
3.4689
3.2906
3.2217
3.1706
3.1218
3.3428
3.7802
4.5759
5.3222
5.6758
6.0151
6.1276
6.1647
6.0552
5.9937
5.9784
5.7171
5.0609
4.8232
4.2979
3.7390
3.3099
2.9529
2.6971
2.6021
2.5640
2.6019
2.6515
2.6531
2.6558
2.7166
2.7408
2.8190
2.8535
2.8639
2.8700
2.7703
2.6353
2.5842
2.5137
2.4497
2.3751
2.3382
2.1323
1.8490
1.6700
1.5507
1.4733
1.4242
1.3643
1.2997
1.2203
1.1462
1.0776
0.9962
0.8265
0.4876
0.1304
0.0341
0.0296
0.0263
0.0261
0.0247
0.0232
0.0256
0.0214
0.0232
0.0208
0.0205
0.0182
0.0186
0.0169
0.0236
0.0198
0.0157
0.0143
0.0179
0.0118
0.0136
0.0139
0.0115
0.0093
0.0096
0.0107
0.0132
0.0090
0.0074
0.0103
0.0071
0.0086
0.0069
0.0052
0.0069
0.0062
0.0115
0.0068
0.0179
0.0121
0.0092
0.0098
0.0138
0.0081
0.0055
0.0077
0.0048
0.0059
0.0052
0.0095
0.0087
0.0114
0.0036
0.0080
0.0110
0.0049
0.0079
0.0065
0.0080
0.0110
0.0059
0.0158
0.0146
0.0095
0.0045
0.0081
0.0116
0.0091
0.0080
0.0095
0.0105
0.0077
0.0098
0.0138
0.0069
0.0118
0.0087
0.0046
0.0056
0.0072
0.0136
0.0110
0.0054
0.0090
0.0147
0.0102
0.0066
0.0102
0.0092
0.0045
0.0089
0.0134
0.0222
0.0336
0.0362
0.0464
0.0354
0.0420
0.0445
0.0400
0.0338
0.0369
0.0441
0.0397
0.0383
0.0353
0.0319
0.0342
0.0366
0.0414
0.0401
0.0452
0.0507
0.0444
0.0358
0.0432
0.0394
0.0406
0.0441
0.0386
0.0410
0.0409
0.0330
0.0282
0.0186
0.0137
0.0103
0.0033
0.0101
0.0080
0.0141
0.0097
0.0102
0.0092
0.0094
0.0055
0.0119
0.0140
0.0116
0.0077
0.0148
0.0063
0.0021
0.0048
0.0033
0.0123
0.0109
0.0108
0.0168
0.0112
0.0046
0.0085
0.0068
0.0091
0.0096
0.0061
0.0063
0.0082
0.0084
0.0094
0.0070
0.0087
0.0042
0.0077
0.0060
0.0123
0.0127
0.0107
0.0019
0.0082
0.0051
0.0068
0.0064
0.0061
0.0057
0.0094
0.0162
0.0141
0.0165
0.0065
0.0121
0.0047
0.0120
0.0076
0.0050
0.0080
0.0139
0.0023
0.0139
0.0123
0.0087
0.0151
0.0060
0.0103
0.0039
0.0042
0.0043
-0.0011
0.0080
0.0028
0.0074
0.0042
0.0018
0.0087
0.0049
0.0076
0.0156
0.0076
0.0091
0.0056
0.0091
0.0075
0.0012
0.0056
0.0123
0.0137
0.0087
0.0025
0.0084
0.0104
0.0086
-0.0008
0.0072
0.0110
0.0096
0.0081
0.0126
0.0020
0.0098
0.0070
0.0041
0.0027
0.0075
0.0040
0.0069
0.0098
0.0180
0.0143
0.0182
0.0120
0.0003
-0.0011
0.0063
0.0104
0.0043
0.0128
0.0075
0.0051
0.0065
0.0063
0.0005
0.0097
0.0099
0.0084
0.0105
0.0017
0.0080
0.0140
0.0054
0.0048