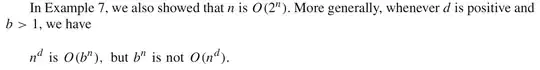How to prove that $n^d$ is $O(b^n)$ from $n$ is $O(2^n)$, given that $d>0, b>1$?

Question

I'm reading Rosen's Discrete Mathematics and Its Application, at Page 212, it's about the "Big-O" notation using in computer science.

This is the description in the book:

And here is my reasoning:

Since there wasn't a program with "negative" steps, I only consider the case $n>0$.

With $n$ is $O(2^n)$, there exist two constants $C$ and $k$ such that $$n \le C \cdot 2^n, \text{when } n>k.$$

Now take logarithms on both side we have $$\log{n} \le \log{C} + n$$

Multiply both side with $d$, we get $$d \cdot \log{n} \le d\cdot \log{C} + d \cdot n,$$

Then I stuck.

Please give me some hints about how to do next... Thanks a lot!

Answer 1

You cannot directly prove $f(n)^d$ is $O(b^n)$ from the fact that $f(n)$ is $O(2^n)$. For example, $2^n$ is $O(2^n)$, but $(2^n)^d$ is not necessarily $O(b^n)$.

So forget the fact that $n$ is $O(2^n)$. You should prove $n^d$ is $O(b^n)$ directly.

You may find a correct proof here.