2

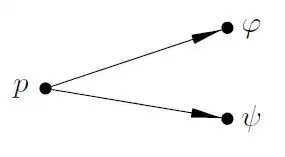
Can someone explain to me (perhaps with an example) why $AF (\phi \lor \varphi)$ is not equivalent to $AF \phi \lor AF \varphi$. This seems counter-intuitive, because in any path where $\phi$ (or $\varphi$) is true, $\phi \lor \varphi$ is true as well. Or is my reasoning wrong?

Thanks

Robin Haveneers
  • 31
  • 2

1 Answers1

4

You also need to argue the other way around. "Each path has either $\psi$ or $\varphi$" is not the same as "either each path has $\psi$ or each path has $\varphi$".

enter image description here

Community
  • 1
Hendrik Jan
  • 31,459
  • 1
  • 54
  • 109