3

I solved this problem using Dynamic Programming in $\mathcal{O}(n)$ time. I found that is equivalent to the Fibonacci Numbers.

$F(0) = F(1) = 1$

$F(n) = F(n-1)+F(n-2)$

Where the $F(n-1)$ term is from fixing the left most domino vertically, and the $F(n-2)$ from fixing it horizontally (which implies that the domino under it must also placed horizontally).

Because the Fibonacci Numbers can be generated in $\mathcal{O}(\lg n)$ using

$F(2n) = F(n)F(n+1)+F(n-1)F(n)$

$F(2n+1) = F(n)F(n)+F(n-1)F(n-1)$

Then I try to find the same expression from the domino tiling. Again, I classify all possible tilings in two set. First, all tiling like the one below Horizontal log n Therefore, $F_H(n) = F(i)F(n-i-2)$. Because I want to split in the middle (or close) I consider $n=2k, i=k$ and $n=2k+1, i=k$. Then

$F_H(2k) = F(k)F(2k-k-2) = F(k)F(k-2)$ and $F_H(2k+1) = F(k)F(2k+1-k-2) = F(k)F(k-1)$.

Then, all tiling of the form 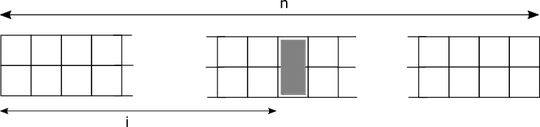Vertical log n Again, $F_V(n) = F(i)F(n-i-1)$ and when $n=2k, i=k$ and $n=2k+1, i=k$ we have

$F_V(2k) = F(k)F(2k-k-1) = F(k)F(k-1)$ and $F_V(2k+1) = F(k)F(2k+1-k-1) = F(k)F(k)$

Combining all the former expressions,

$F(2k) = F_H(2k) + F_V(2k) = F(k)F(k-2) + F(k)F(k-1)$

$F(2k+1) = F_H(2k+1) + F_H(2k+1) = F(k)F(k-1) + F(k)F(k)$

However, those final expression does not produce the same numbers. Because they look really similar I belive my approach is not completly wrong but I can not find where I make my mistake.

Final notes:

  1. In the first classification, I fix the top most domino horizontally and if I consider a 1-tile shifted horizontal domino (left or right) under it, then the rectangle can not be tiled.
  2. For the (correct) expression $F(2n+1)=F(n)F(n)+F(n-1)F(n-1)$, notice that $F(n)F(n)$ can be mapped to the second case, because $n+1+n = 2n+1$, but the other term $F(n-1)F(n-1)$ can not (at least in the same way), $(n-1)+2+(n-1)\neq 2n+1$. The same can be notice in $F(2n)$ and again one term can be mapped to the second case while the other can not (to the first case). I belive my mistake should be around the first case.
Black Arrow
  • 243
  • 1
  • 6

1 Answers1

3

In your second attempt you tried to fixate the $(k+1)$th term. But instead of the two cases

1 2 ... k k+1 k+2 ... n
           | 
           |

and 

1 2 ... k k+1 k+2 ... n
           ----- 
           -----

there exist a third case:

1 2 ... k k+1 k+2 ... n
        ---- 
        ----

So if $n = 2 k$, then you have $f(k)f(k-1)$ for the first case, $f(k)f(k-2)$ for the second one, and $f(k-1)f(k-1)$ for the third one. This gives in total:

$f(2k) = f(k)f(k-1) + f(k)f(k-2) + f(k-1)f(k-1) = f(k)[f(k-1) + f(k-2)] + f(k-1)f(k-1) = f(k)^2 + f(k-1)^2$.

Now this formula looks like the formula for $F(2n+1)$ that you posted.

Because the Fibonacci Numbers can be generated in O(lgn) using

F(2n)=F(n)F(n+1)+F(n−1)F(n)

F(2n+1)=F(n)F(n)+F(n−1)F(n−1)

Simple reason: the formula assumes that $F(1) = F(2) = 1$ while you have $f(0) = f(1) = 1$. So after an index shift it should match.

Identical procedure for the odd case $n = 2k + 1$.

edit: Tried to do the index shift but failed. Reason was, that you wrote down the wrong formula for $F(2n+1)$. It should be $F(2n+1)=F(n)^2+F(n+1)^2$. Then the index shift works:

$f(2k) = F(2k+1) = F(k)^2+F(k+1)^2 = f(k-1)^2 + f(k)^2$.

Jakube
  • 1,605
  • 10
  • 14