My definition says
A clique is a graph that has an edge connecting every pair of vertices
but as I understand, an edge connects only two vertices. Like $A-B$.
If we want to connect three vertices, we need at least two edges. For example, $A-B-C$.
I don't understand how an edge can connect every pair of vertices.
Recalling that a clique is a subset $C$ of vertices of an undirected graph such that the subgraph induced by $C$ is fully connected. That is, every two distinct vertices in $C$ are connected by a distinct edge of the graph. This means different edges, not the same.
So, on a clique $C$ containing $k$ vertices $v_1, v_2,..,v_k$, there are $\frac{k(k-1)}2$ edges connecting them, that is the number of possible unordered pairs on $k$ elements.
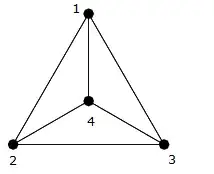
As you can see in the previous picture, this is a clique on four vertices $\{{1,2,3,4}\}$, so there is a different edge connecting every edge (i.e. $(1,2)$,$(1,3)$,$(1,4)$,$(2,3)$,$(2,4)$,$(3,4)$).
You can count them and see that there are exactly $6 = \frac{4\times 3}{2}$ edges.
