I can think of a O(n log n) solution:
- Input: the set of all 2-D points on your graph in the form of
(a, b) - where a is the x-coordinate and b is the y-coordinate. Assumption: points are unique. O(n)
- Build a HashTable to count the occurrences of each distinct y-coordinate,
b, over this set. (i.e. b is the key and its occurrence is the value) For example: 5 total points with b==3, 4 total points with b==7, etc. O(n)
- Sort the HashTable in descending order on
b, based on its occurrence count: largest occurrence count first. O(n log n)
- While number of x that have points is still more than X/2, loop: O(n)
- Remove the top entry in the sorted result from the HashTable O(1)
- (number of x remaining) = (number of x remaining) - corresponding occurrence count with this entry. O(1)
- Increment a count of how many entries removed so far O(1)
- Output the count of how many entries removed, and that is the minimum number of y's that you have to remove to get number of x's that have points less than X/2
Total complexity:
- Runtime: O(n log n)
- Space: O(n) (to store input and to build the HashTable)
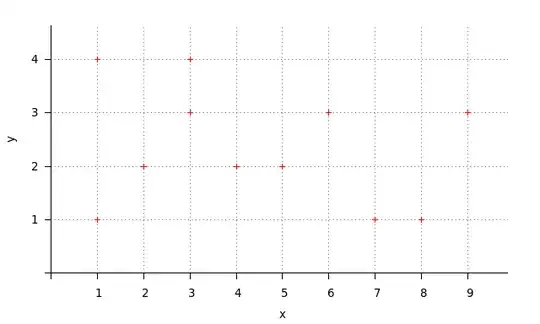
Here's a walkthrough of the algorithm with the example provided by your image:
We have as input the points:
(1, 1)
(1, 4)
(2, 2)
(3, 3)
(3, 4)
(4, 2)
(5, 2)
(6, 3)
(7, 1)
(8, 1)
(9, 3)
Putting the y-coordinates b into a HashTable with b as the key and its occurrence as the value:
{
"1": 3,
"2": 3,
"3": 3,
"4": 2,
}
This is a sorted order based on the occurrence count, so we first remove y at 1, this removes the points:
(1, 1)
(7, 1)
(8, 1)
and then move y at 2:
(2, 2)
(4, 2)
(5, 2)
and we are done.