as the title suggests, I was struggling to define the differences between finite and Büchi automata and how they are represented.
From an assignment I'm working on, this automaton can be depicted as both infinite automaton and Büchi automaton.
Can you give me an example for each of those automatons to understand the differences?
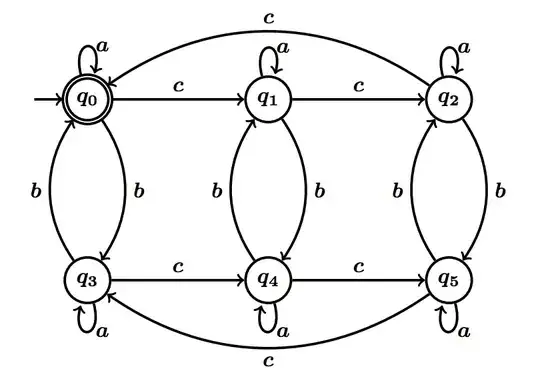
The automaton models themselves, that is the syntax, are indeed identical: both have a finite set of states, a transition relation, and initial and final state(s).
The difference lies in the acceptance criteria, that is the semantics.
A finite automaton $A$ accepts a word $w$ if and only if there is a computation¹ for $w$ in $A$ that ends in a final state.
A Büchi automaton $B$ accepts a word $w$ if and only if there is a computation¹ for $w$ in $B$ that visits final states infinitely often².
The differences follow from this.
There is no difference in the specification (syntax). The only difference is in the interpretation (semantics). The language accepted by a DFA consists of finite strings defined in a certain way given the DFA, and the language accepted by the corresponding Büchi automaton consists of infinite strings defined in a certain way.
Indeed, you can leverage this connection to prove results such as:
An $\omega$-language is recognizable by a deterministic Büchi automaton iff it is the limit language of some regular language.
For a proof, see Wikipedia.
There are two main differences. First, finite automata are used to recognize sets of finite words and Büchi automata are designed to recognize sets of infinite words. The second main difference is that finite deterministic and finite nondeterministic automata have the same expressive power: both accept the regular languages, but the situation is different for Büchi automata: as Yuval Filmus pointed out, deterministic Büchi automaton accept the limit of regular languages, but nondeterministic automata accept the whole class of $\omega$-regular languages and these two classes are distinct. However, there do exist classes of deterministic $\omega$-automata that recognize exactly the class of $\omega$-regular languages, for instance Muller automata, parity, Rabin, or Streett automata.
