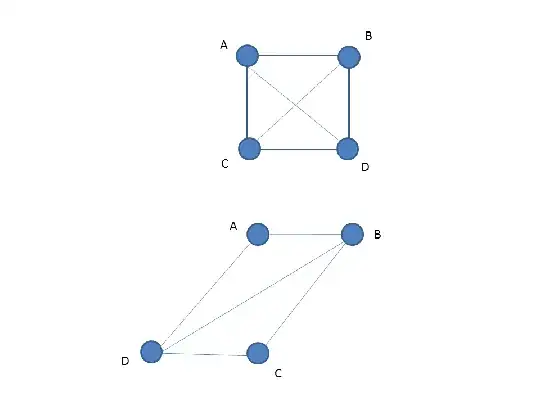
As part of a larger problem, I am trying to detect based on the distance matrix which segments intersect in the original 2D space that originated the matrix. I don´t have coordinates (lat/long, x/y or any other for the points).
As an example, on the image below, the answer to the question for the top graph would be: AD, BC. While for the bottom graph would be AC, BD.
The information that we have is just the distance matrix:
DISTANCE MATRIX TOP
$ \begin{align} && A && B && C && D \\ A&& 0 && 1 && 1 && \sqrt{2} \\ B&& 1 && 0 && \sqrt{2} && 1 \\ C&& 1 && \sqrt{2} && 0 && 1 \\ D&& \sqrt{2} && 1 && 1 && 0 \end{align} $
DISTANCE MATRIX BOTTOM
$ \begin{align} && A && B && C && D \\ A&& 0 && 1 && 1 && \sqrt{2} \\ B&& 1 && 0 && \sqrt{2} && \sqrt{5} \\ C&& 1 && \sqrt{2} && 0 && 1 \\ D&& \sqrt{2} && \sqrt{5} && 1 && 0 \end{align} $
I have tried so far to use the triangular inequality and some other (probably) naive geometric knowledge but I can´t figure out what conditions must be met.