Fast algorithm for clustering groups of elements given their size/time

Question

I don't know if there is a canonical problem reducing my practical problem, so I will just try to describe it the best that I can.

I would like to cluster files into the specified number of groups, where each groups size (= the sum of sizes of files in this group) is as close as possible to each other group in this cluster (but not in other clusters). Here are the requirements:

1. The first group always contain one file, which is the biggest of all groups in the cluster.
2. Any other group but the first can have multiple files in it.
3. The number of groups in each cluster is constrained to a maximum specified by user (but there can be less groups if it's better or there's not enough files).
4. There's no constraint on the number of clusters (there can be as little or as many as necessary).
5. Goal (objective function): minimize the space left in all groups (of all clusters) while maximizing the number of groups per cluster (up to the maximum specified).

The reason behind these requirements is that I am encoding files together, and any remaining space in any group will need to be filled by null bytes, which is a waste of space.

Clarification on the objective and constraints that follow from the requirements and the problem statement:

• Input is a list of files with their respective size.
• Desired output: a list of clusters with each clusters being comprised of groups of files, each group having one or several concatenated files.
• There must be at least 2 groups per cluster (except if no file is remaining) and up to a maximum of G groups (specified by user).
• Each file can be assigned to any group whatsoever and each group can be assigned to any cluster.
• The number of clusters can be chosen freely.

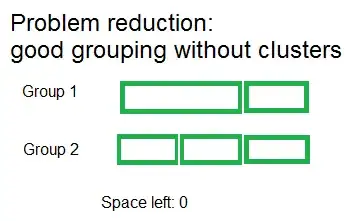
Here is a schema that shows one wrong and one good example of clustering schemes on 5 files (1 big file, and 4 files of exactly half the size of the big file) with a number of groups = 2:

The solution needs not be optimal, it can be sub-optimal as long as it's good enough, so greedy/heuristics algorithms are acceptable as long as their complexity is good enough.

Another concrete example to be clear: let's say I have this list of 10 files with their sizes, this is the input (in Python):

['file_3': 7,
'file_8': 11,
'file_6': 14,
'file_9': 51,
'file_1': 55,
'file_4': 58,
'file_5': 67,
'file_2': 68,
'file_7': 83,
'file_0': 85]

The final output is a list of clusters like this (constrained here to 3 groups per cluster):

{1: [['file_0'], ['file_7'], ['file_2', 'file_6']],
 2: [['file_5'], ['file_4', 'file_3'], ['file_1', 'file_8']],
 3: [['file_9']]}

And for example here (this is not a necessary output, it's just to check) the total size of each groups (ie, sum of file sizes for each group) for each cluster:

{1: [85, 83, 82], 2: [67, 65, 66], 3: [51]}

If the problem is NP-complete and/or impossible to solve in polynomial time, I can accept a solution to a reduction of the problem, dropping the first and fourth requirements (no clusters at all, only groups):

Here is the algorithm I could come up with for the full problem, but it's running in about O(n^g) where n is the length of the list of files, and g the number of groups per cluster:

Input: number of groups G per cluster, list of files F with respective sizes
- Order F by descending size
- Until F is empty:
    - Create a cluster X
    - A = Pop first item in F
    - Put A in X[0] (X[0] is thus the first group in cluster X)
    For g in 1..len(G)-1 :
        - B = Pop first item in F
        - Put B in X[g]
        - group_size := size(B)
        If group_size != size(A):
            While group_size < size(A):
                - Find next item C in F which size(C) <= size(A) - group_size
                - Put C in X[g]
                - group_size := group_size + size(C)

How can I do better? Is there a canonical problem? It seems like it's close to scheduling of parallel tasks (with tasks instead of files and time instead of size), but I'm not quite sure? Maybe a divide-and-conquer algorithm exists for this task?

Answer 1

Finally I could devise a better algorithm by turning the problem upside down (ie, using bottom up construction instead of top-down).

In my OP algo, I first create a cluster and its groups, and then I walk through the whole files list until I could either fill completely the groups sizes, or there's no file in the files list small enough to fit.

Here it's the other way around: I walk through the files list, and for each file I either assign it to a group if it fits, or if it's too big I create a cluster and init it with this file. To do that, I continually maintain a list of groups sizes to fill, using insertion sort so that when I pick a file to organize, I just need to check its size against the first item of the "to-fill" list.

Here's the algorithm, running in O(n log(g)) (thank's to insertion sort or binary search trees):

For each file:
    - If to-fill list is empty or file.size > first-key(to-fill):
      * Create cluster c with file in first group g1
      * Add to-fill[file.size].append([c, g2], [c, g3], ..., [c, gn])
    - Else:
      * ksize = first-key(to-fill)
      * c, g = to-fill[ksize].popitem(0)
      * Add file to cluster c in group g
      * nsize = ksize - file.size
      * if nsize > 0:
        . to-fill[nsize].append([c, g])
        . sort to-fill if not an automatic ordering structure

Since it's running in O(n log(g)), the number of groups has little impact on the running time, contrary to the algo in the OP. Maybe it's possible to do better, but for now it is fast enough for me, since it can reasonably work on lists of 10M files under 20 seconds.

For those interested, here's a working implementation in Python (I used the sortedcontainers module for the sorted list, which runs in O(log(g)) instead of O(g) for insertion sort):

from collections import OrderedDict
from random import randint
from lib.sortedcontainers import SortedList

def gen_rand_fileslist(nbfiles=100, maxvalue=100):
    fileslist = {}
    for i in xrange(nbfiles):
        fileslist["file_%i" % i] = randint(1, maxvalue)
    return fileslist

def group_files_by_size_fast(fileslist, nbgroups, mode=1):
    '''Given a files list with sizes, output a list where the files are grouped in nbgroups per cluster.'''
    For each file:
        - If to-fill list is empty or file.size > first-key(to-fill):
          * Create cluster c with file in first group g1
          * Add to-fill[file.size].append([c, g2], [c, g3], ..., [c, gn])
        - Else:
          * ksize = first-key(to-fill)
          * c, g = to-fill[ksize].popitem(0)
          * Add file to cluster c in group g
          * nsize = ksize - file.size
          * if nsize > 0:
            . to-fill[nsize].append([c, g])
            . sort to-fill if not an automatic ordering structure
        '''
    ftofill = SortedList()
    ftofill_pointer = {}
    fgrouped = [] # [] or {}
    ford = sorted(fileslist.iteritems(), key=lambda x: x[1])
    last_cid = -1
    while ford:
        fname, fsize = ford.pop()
        #print "----\n"+fname, fsize
        #if ftofill: print "beforebranch", fsize, ftofill[-1]
        #print ftofill
        if not ftofill or fsize > ftofill[-1]:
            last_cid += 1
            #print "Branch A: create cluster %i" % last_cid
            fgrouped.append([])
            #fgrouped[last_cid] = []
            fgrouped[last_cid].append([fname])
            if mode==0:
                for g in xrange(nbgroups-1, 0, -1):
                    fgrouped[last_cid].append([])
                    if not fsize in ftofill_pointer:
                        ftofill_pointer[fsize] = []
                    ftofill_pointer[fsize].append((last_cid, g))
                    ftofill.add(fsize)
            else:
                for g in xrange(1, nbgroups):
                    try:
                        fgname, fgsize = ford.pop()
                        #print "Added to group %i: %s %i" % (g, fgname, fgsize)
                    except IndexError:
                        break
                    fgrouped[last_cid].append([fgname])
                    diff_size = fsize - fgsize
                    if diff_size > 0:
                        if not diff_size in ftofill_pointer:
                            ftofill_pointer[diff_size] = []
                        ftofill_pointer[diff_size].append((last_cid, g))
                        ftofill.add(diff_size)
        else:
            #print "Branch B"
            ksize = ftofill.pop()
            c, g = ftofill_pointer[ksize].pop()
            #print "Assign to cluster %i group %i" % (c, g)
            fgrouped[c][g].append(fname)
            nsize = ksize - fsize
            if nsize > 0:
                if not nsize in ftofill_pointer:
                    ftofill_pointer[nsize] = []
                ftofill_pointer[nsize].append((c, g))
                ftofill.add(nsize)
    return fgrouped
fgrouped2 = group_files_by_size_fast(fileslist, nbgroups)

def grouped_count_sizes(fileslist, fgrouped):
    '''Compute the total size per group and total number of files. Useful to check that everything is OK.'''
    fsizes = {}
    total_files = 0
    allitems = None

    for fkey, cluster in enumerate(fgrouped):
        fsizes[fkey] = []
        for subcluster in cluster:
            tot = 0
            for fname in subcluster:
                tot += fileslist[fname]
                total_files += 1
            fsizes[fkey].append(tot)
    return fsizes, total_files

if __name__ == '__main__':
    nbfiles = 10000000
    nbgroups = 10
    fileslist = gen_rand_fileslist(nbfiles)
    fgrouped = group_files_by_size(fileslist, nbgroups)
    fsizes, total_files = grouped_count_sizes(fileslist, fgrouped)
    print total_files
    print fsizes

Answer 2

You should look at bin-packing algorithms. Yours is simple as the constraint is only on 1 dimension, the size of the elements. But you have more complex ones with multiple dimensions. I paste the wikipedia here as a start but you can find lots of resources online as it's a famous algorithmic problem