How to choose between several constraints for a SAT task using quality metric?

Question

I'm trying to solve a constraint programming problem using a SAT solver. I have set of constraints in the form of propositional logic statements, which are converted to CNF using Tseitin transformation. A number of inputs are fixed and pretty large - up to ~30k. A number of constraints can be ~200k.

Right now, I have to choose between several constraint candidates which will be added to the CNF formula. All of them have some quality parameter - basically, a candidate should not remove too many feasible solutions from a search space. I can choose between smaller rules (a few boolean operators like AND, OR and no more than 10 inputs), but it is just impossible for the larger constraints (dozens of operators and ~100 inputs), there is no way to predict the quality of solution in that case. So, I ended up with the idea of a tool, which will automatically choose the best option for me.

For example, I have the basic rule: $$\neg(A \wedge B \wedge(C \vee D \vee E))1)$$ For this rules, I have two corresponding additional rules and I have to choose one of them: $$\neg(A \wedge B) \wedge blah2)$$ $$\neg (C \vee D \vee E) \wedge blah3)$$ The (2) formula is the best for me - it removes lesser number of solutions. blah is not relevant to my question, but it always appears inside candidates.

What I have tried already:

1. Use Espresso logic minimization tool. I input all candidates at ones and hope to get the minimal representation. It kind of works, but the tool ignores a quality metric - the result is too constraining for my problem. Too many possible solutions are prohibited. In addition, my problem is far too big for Espresso and I have to use it in incremental manner. I assume that is an issue too - Espresso does not see the whole picture at ones.

2. SAT solvers or model counting. The idea is the following - estimate a number of possible solutions under some basic constraints. I can add one of the candidates, estimate a number of possible solutions again, remove it and run such a procedure for each candidate. Eventually, I can choose one with the largest number of legal solutions. It seems to be working, however, it is too slow with real cases - exact counter freezes forever, approximate counter concludes that there are infinite number of solutions.

I would like to brainstorm that problem - maybe someone can propose interesting formulation/approaches for this task? May it can be formulated as ILP task somehow?

UPDATE: I am given a geometry problem - i have a rectangular tile that should be filled with a set of various objects. Some configurations of objects are prohibited (it does not matter why). Each rule is populated in every applicable point of a tile: 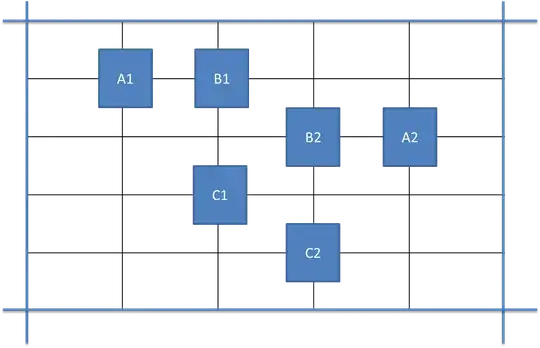$$\psi = \neg (A_1 \wedge B_1 \wedge C_1) \wedge \neg (A_2 \wedge B_2 \wedge C_2)$$

Blue bold lines are tile's borders. Such configuration of objects is prohibited: $$ \neg (A \wedge B \wedge C) 4)$$ This fact is represented as a set of clauses. $\psi$ forms a SAT task. You can think of it like "SAT, find me a tile which does not have any of these prohibited configurations". And this is my core formula. The same rule in different points of tile forms an identical set of clauses, but over different variables, e.g. $A_1, B_1, C_1$ and $A_2, B_2, C_2$ in the formula above - one rule forbids a set of 3 objects in 2 different points.

At the same time, such rules can be partially outside a tile (pay attention to the right side border). The object outside is transparent:

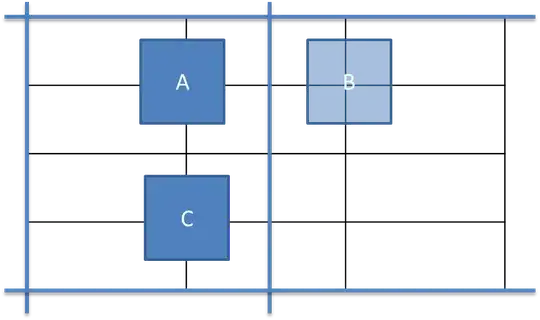
This is prohibited too. The issue is that SAT solver does not know anything about world outside a tile, there is literally nothing out there. However, I still need to capture such configurations. I take each core rule and split it with boundary: 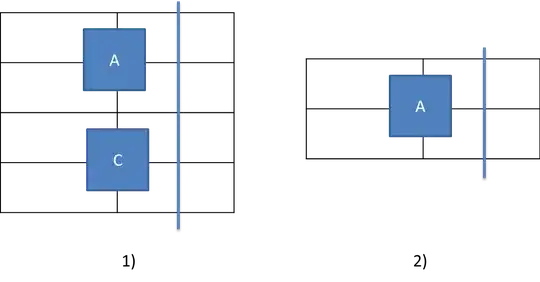$$\neg(A \wedge boundary) 5)$$ $$\neg(A \wedge C \wedge boundary) 6)$$

Over the whole tile it looks like this:

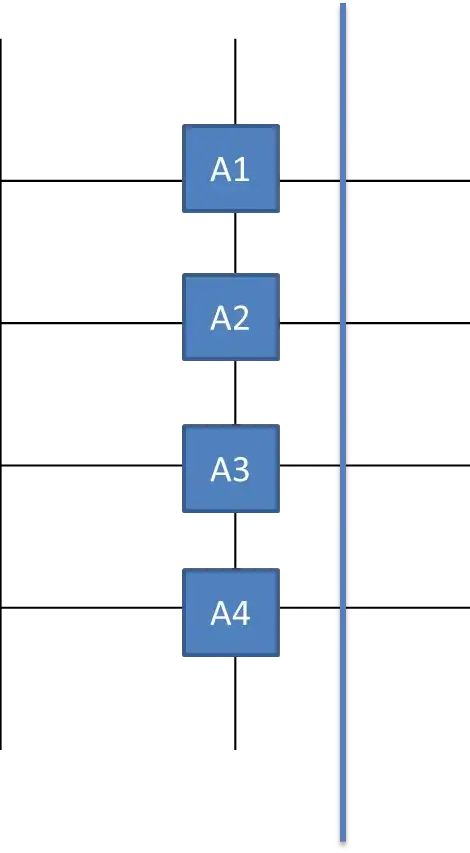
If we choose 5) rule, we will prohibit all obects $A$ near the boundary: $$\psi = \neg (A_1 \wedge boundary) \wedge \neg (A_2 \wedge boundary) \wedge \neg (A_3 \wedge boundary) \wedge \neg (A_4 \wedge boundary)$$

However, we can choose 6) rule: $$\psi = \neg (A_1 \wedge A_2 \wedge boundary) \wedge \neg (A_2 \wedge A_3 \wedge boundary) \wedge \neg (A_3 \wedge A_4 \wedge boundary)$$ This option is much better - it prohibits 2) rule near the boundary already and at the same time it allows to place single $A$ object near the boundary.

My questions:

1. How can I choose between various candidates?
2. Which tools can me help? #SAT, MaxSAT, MIP?
3. Which metric can I use to optimise a set of rules?

Answer 1

It appears that your problem is the following:

Input: boolean formulas $\Phi,\Psi_1,\dots,\Psi_k$
Output: a set $S \subseteq \{1,\dots,k\}$ whose size is as large as possible, such that $\Phi \land \land_{i \in S} \Psi_i$ is satisfiable

This problem can be formulated as an instance of MAX-SAT, specifically PMAX-SAT, and then solved using a MAX-SAT solver.

In particular, introduce boolean variables $t_1,\dots,t_k$. Define the formula $\Gamma$ to be the result of converting

$$\Phi \land \bigwedge_i (t_i \implies \Psi_i)$$

to CNF form. Now create the conjunction $\Gamma \land t_1 \land \dots \land t_k$, and ask the solver to choose a subset of the clauses $t_1 \land \dots \land t_k$ that makes conjunction satisfiable. (You mark the clauses of $\Gamma$ as required and ask it to find a subset of the remaining clauses.) This is an instance of MAX-SAT; and its solution corresponds to a solution to the original problem.

Alternatively, you can express it as an instance of weighted MAX-SAT. As before, use the conjunction $\Gamma \land t_1 \land \dots \land t_k$, but now give every clause in $\Gamma$ some large weight $W$ (chosen so that effectively, $\Gamma$ is forced to be satisfied) and each clause $t_i$ weight 1. This is an instance of weighted MAX-SAT; and its solution corresponds to a solution to the original problem.

---

I'm not sure why your #SAT solver was returning "infinity". Maybe you need to find a better solver for #SAT. Actually, approximate-#SAT would be good enough for your needs. See e.g. Is there a sometimes-efficient algorithm to solve #SAT? and Using SMT solvers to generate random solutions to given predicate for some relevant literature and techniques.