Convert the language into CNF or DNF form

Question

A boolean circuit C has n inputs and m outputs, and is constructed with AND, OR, and NOT gates. Each gate has fan-in 2 except the NOT gate which has fan-in 1. The out-degree can be any number. A circuit is not allowed to have any cycles.

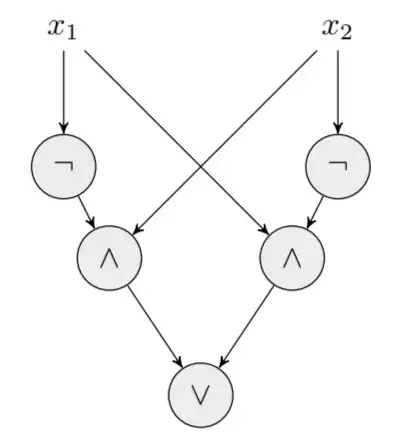
For example construction of a circuit C computing the XOR function, i.e., $C(x_1, x_2) = 1 \iff x_1\neq x_2:$

I need to construct a circuit family for language $L=\{\langle k, m, j \rangle|(k+m)[j]=1\}.$ That means, we need to construct the circuit which checks whether the $j$-th bit of the sum of given binary numbers $k$ and $m$ is $1$.

My question is how to represent the $L$ as a expression of CNF form or DNF form by which I can easily construct the circuit?

Answer 1

I suggest you learn how to build a circuit for addition (this is well described in textbooks), and how to build a circuit for a demultiplexer (also well described), and then you should be able to solve your problem on your own.

CNF/DNF form are unlikely to be helpful here.