Closest point on a convex hull in log(n)

Question

We are given a convex polygon $C = \{P_1, P_2, \dots, P_n\}$, where the points are ordered either clockwise or counter-clockwise. Additionally, we have a point $P_\text{new} = (x, y)$ that lies outside the convex hull. The goal is to find the point $P_i$ in $C$ that is closest to $P_\text{new}$ in a logarithmic time complexity. ($O(\log n)$.)

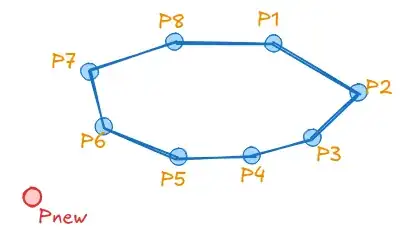
We can't use sorting because that would take $O(n \log(n))$ time, and also we can't use binary search because of the shape of a convex hull and we might delete the half that contains the answer.

Answer 1

We'll assume that we need to find a vertex $P_i$ of the convex polygon $C$, closest to the external (to the polygon) point $Q$, provided that the segment $\overline{P_i Q}$ lies outside of the polygon.

• Step 1. Find left and right tangent line from the point $Q$ to the polygon $C$. That can be done in $O(log(n))$ time for convex polygons - for example, see here. Two tangent lines correspond to two vertices $(P_{left},P_{right})$ of the polygon $C$. These vertices divide the polygon into two polylines - visible from the point $Q$, and invisible from this point.

• Step 2. We need to look for the closest vertex in the visible polyline only. The distance from the vertex $P_k$ to the point $Q$ as a function of index $k \in [left, right]$ is unimodal (has a single minimum) - so we can use Ternary Search to find this minimum. This search takes $O(log(n))$ time as well.

Q.E.D.

Answer 2

Start of an answer:
Given $P_{new}$ outside

1. a regular $(2n+1)$gon (simple case):
   Pick an edge $e$ and its vertices $v_a$ and $v_b$.
   If their distances to $P_{new}$ are equal,
   either both are closest to $P_{new}$, or the vertex $v_{oe}$ opposite to $e$ is.
   Else the closest vertex is between $v_{oe}$ and the closer of $v_a$ and $v_b$, to be found using binary search.
2. part of a regular polygon:
   Start with a wedge-shaped third of a regular polygon with lots ( $n - 1$) of vertices on the outcircle and one incident to the centre. Now move "the tip vertex" $v_t$ a bit closer to the segment; $P_{new}$ is somewhere between $v_t$ and the centre. For good measure, move every third vertex slightly inward (such that it is just outside the chord through its neighbours).
   What makes this case look hard?
   Start at one of the vertices moved inward, say, $v_i$, the next counter-clockwise from the one opposite to $v_t$:
   both its neighbours will be farther from $P_{new}$. Worse, the ninth in both directions, while local minima of distance too, will be farther than $v_i$, too.