Find a minimal (irregular) boundary over a grid of colored cells

Question

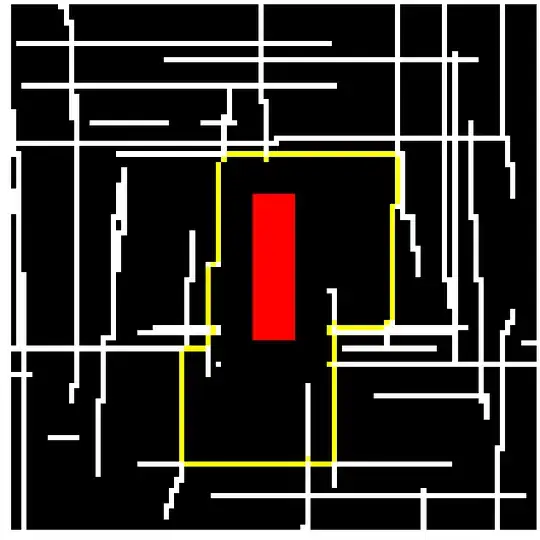
A grid is divided up into red cells (pixels), black cells, and white cells. We want to find the smallest boundary that:

1. All red cells are within the boundary
2. All cells of the boundary itself are white

The boundary can be irregular, but it must be continuous - no gaps or holes.

What algorithm can do this?

What happens if we require the boundary to be convex?

Background: The motivation came from What algorithm can expand find the irregular boundary around a drawing on a printed page?

By continuous I mean that starting from any pixel in the boundary, you can walk to any other pixel in the boundary, while never having to leave the boundary. By smallest I mean smallest area (though I conjecture it's stronger than that: I conjecture there is a boundary $S$ that any other boundary needs to include.)

(In response to a question:) We can simplify the problem by assuming: All red cells form a single axis-aligned rectangle.

Answer 1

Either I do not understand your problem, or the problem is solved by using a BFS/DFS from the red cells. There must be a unique solution if it exists, since if two areas with crossing boundaries exist, you can take the innermost boundaries.

The solution is therefore to run a BFS starting from the red cells, and not crossing over a white cell.

This is the solution when "smallest boundary" means "smallest area" as you have pointed out. If you rather want the boundary with the fewest possible cells, it corresponds to a minimum cut.

Responding to the comment: in the bfs, initiate the queue with all red vertices. Now, for each new vertex you expand, if it is white, do not add its neighbourhood to the queue.

For simplicity, assume your instance is embedded in an infinitely large black grid. If there is a solution, then the BFS will stop because there exists a separator of white cells that the search cannot cross. Now, whenever you find a solution, the boundary has to be white since if it contained a black vertex the search would not have stopped at that cell, but also added its neighbor (on the outside of the boundary) to the queue.

Here is an illustration where we run BFS from the red rectangle, not crossing white cells. The yellow cells form the boundary. As you can imagine, if there were a "white shortcut" through the inside of the boundary, that would form a smaller area and we would choose that instead: