I encountered this problem while doing some “graph”ics programming:
Take a directed acyclic graph where every vertex is given a non-unique label 1..N
You can ‘trim’ the DAG by making a cut that removes all vertices that share one label and also don’t have any ancestors of a different label. Repeat until the DAG is empty.
I’m trying to find an efficient algorithm that finds the minimal number of trims. I'm looking for algorithms that find the correct optimal answer, rather than heuristics.
Below is an example of the process.
- Start with the DAG on the left
- Trimmed blue that don't have non-blue ancestors
- Trimmed all red since now both don't have any non-red ancestors
- Trimmed all green since now they don't have any non-green ancestors
- Trimmed the remaining blue that now don't have non-blue ancestors
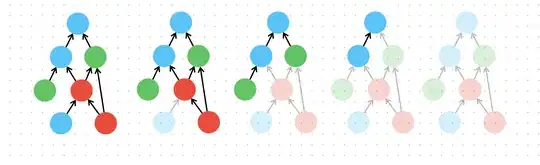This is the optimal trimming order in this case.
If instead you started by trimming red first you could only remove one red vertex (the one that doesn't have a blue ancestor) and you would end up with more trimming steps.
A decent heuristic I found is to sort by label, then stably topologically sort, but it doesn’t give an optimal solution. But it made me realize another way to frame the problem: How do we find a topological sort of a DAG that when read from one end to another changes labels the least number of times.
Here’s the source of the problem if you’re curious: I’m drawing 2D primitive shapes on a screen (circle, square, etc) and it’s more efficient to batch draw shapes of the same type. However the shapes can overlap and the batches I’m making have to respect the overlaps. Each shape is a vertex, each shape type is a label and a directed edge is added when one shape overlaps another.
So e.g. I first draw all the circles that don’t overlap any other shape (though they can overlap each other). Then draw a bunch of squares that may have overlapped the first batch of circles, then I draw another batch of circles that overlapped the squares.
