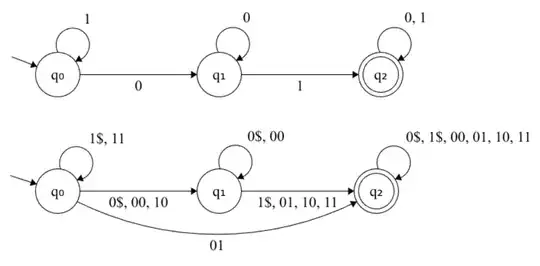
I found this function that can be applied onto a DFA to produce a DFA. Is there a name for it?
Above: A simple DFA over the alphabet $\{0, 1\}$
Below: The resultant DFA over the alphabet $\{0\mathrm{$}, 1\mathrm{$}, 00, 01, 10, 11\}$
You can think of the result as a speedup of the original DFA. Loosely, the resultant DFA processes its input two characters at a time. The transition function encodes walks of length two. The input characters are grouped into pairs. If the string is odd, the final character is grouped with a new special character $\\\$$ denoting the end of the string. Formally, if the original alphabet is $\Sigma$, then the transformed alphabet is $(\Sigma \times (\Sigma \cup \{ \mathrm{$} \})$.