2

According to the theorem(see reference) on the rigidity of frameworks:

A rectangular framework is rigid if and only if its associated bipartite graph is connected.

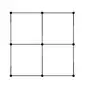
Now consider the case for a 2-by-2 rectangular framework.

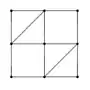
enter image description here enter image description here

In this case, if we draw a brace in the first and the third squares, the framework becomes rigid (since, by observation, none of the smaller squares can be skewed without skewing the braced squares).

However, the resulting bipartite graph is not a connected one. Since the theorem establishes an one-to-one correspondence between the associated bipartite graph being connected and the rigidity of framework, the example that I have come up here surely violates the theorem.

enter image description here

What am I getting wrong here?

Reference:

Theorem 1.4.1, Gross, J. L., & Yellen, J. (2005). Graph Theory and Its Applications. In Chapman and Hall/CRC eBooks. Informa. https://doi.org/10.1201/9781420057140

Aniruddha
  • 143
  • 6

1 Answers1

1

The picture shows that the given framework is not a rigid framework since it can be skewed in the following manner:

enter image description here

Inuyasha Yagami
  • 6,277
  • 1
  • 12
  • 23