Case 1: Union of selected intervals might not be a single interval
First of all, sort the intervals in increasing order of $I_i.start$
Use the following Dynamic Programming solution:
$$
\mathrm dp(i, j, k) = max(
\text{extend_union} + dp(i + 1, j’, k - 1), dp(i + 1, j, k) )
$$
where
$$
\mathrm j' = \begin{cases}
i & \text{if } I_i.end > I_j.end \\ % & is your "\tab"-like command (it's a tab alignment character)
j & \text{otherwise.}
\end{cases}
$$
$$
\mathrm extend\_union = \begin{cases}
max(0, I_i.end - I_j.end) & \text{if } I_j \text{ intersects }I_i \\ % & is your "\tab"-like command (it's a tab alignment character)
I_i.end - I_i.start & \text{otherwise.}
\end{cases}
$$
$dp(i, j, k)$ denotes the maximum sum of lengths of the segments in the
range the $[i, N)$
$j$ is the range $I_j$ such that $I_j.end$ is the maximum among all the segments that we chose until now
$k$ denotes how many more segments are left to choose.
We have 2 choices at each state
Choice 1: Consider the interval $I_i$ in our subset.
In this case, the union length will increase by the amount $\text{extend_union}$ as mentioned above
Choice 2: Don't consider the interval $I_i$ in our subset.
In this case, the union length will not increase
If you have reached, with $i=N$ and $k=0$, return $0$ else $-\infty$
Time Complexity: $O(N^2K)$
Case 2: Union of selected intervals should be a single interval
First of all, sort the intervals in increasing order of $I_i.start$
- Now, create a graph of $N$ nodes such that for every $i$, there an edge from $i$ to $j$ $(i < j)$ such that
$j = \underset{j}{\operatorname{argmax}} I_j.end$ where $I_i \bigcap I_j \neq \phi$ and $I_j.end > I_i.end$.
Don't add an edge if such $j$ doesn't exist
This $j$ can be found out using any range querying data structure like segment trees in $O(log(N))$ or in $O(1)$ with sparse tables and precomputations
This will add $O(N)$ edges in the graph
- The resulting graph will be a DAG, with at most one path between any pairs of nodes $i$ to $j$
- It will be similar to this:
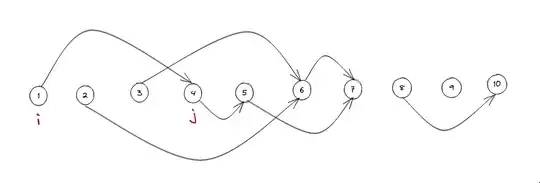
- Now, if we choose any starting node in this graph and traverse $K$ nodes to the right, we will end with the most optimal subset of size $K$ having a certain union length. We can use this to maximize the answer
- It may happen that there are $M < K$ nodes to traverse, in that case, we can consider this subset only if there are $K-M$ other intervals that lie within this union.
Finding these $K-M$ other intervals may take $O(N)$ time in the worst case
To speed this up, the following observations are helpful:
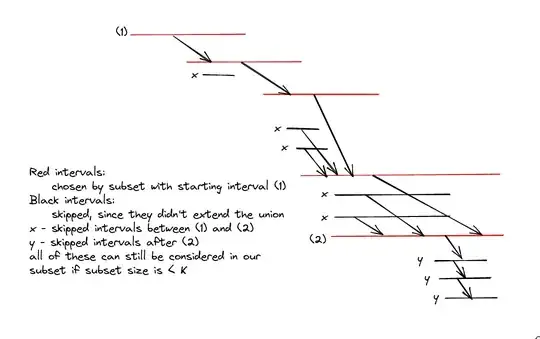
From the image above, if number of x segments + number of y segments is $\geq K-M$, this subset can be consider in our answer
- Let $l$ be the index of starting interval of our subset and $r$ be the index where we end up in this case
- Notice that number of x segments is simply $(r - l + 1) - M$, computing in $O(1)$ time
To find the number of y segments, we can use binary search to find the rightmost index $id$ in the range $[r+1, N]$ and $I_{id}$ lies within $I_r$
- Then the number of y segments is simply $id - r$, computed in $O(log(N))$ time
- We can use the binary search here because the interval $I_r$ can no longer extend further and the ranges after that will lie completely within the interval $I_r$ or start anywhere $> I_r.start$
If that is the case we can update the answer with the union length of this subset
- Considering every interval as the starting point of the subset and traversing $K$ nodes each time will result in $O(N*K$) time
- To optimize it further, notice that we only require the starting and ending indices and not the entire subset indices. Furthermore, nodes chosen by a subset can be reused by other subsets based on their connectivity in the DAG that we defined above
- Instead of adding the edges from $i$ to $j$, we keep them from $j$ to $i$. This is because the resultant disjoint trees formed will have their roots(nodes that don't go further) to the right. The following diagram depicts what we are doing:
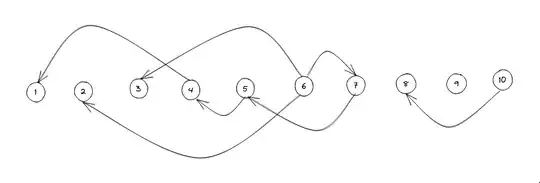
- DFS on nodes indexed from $N$ to $1$ and keep a list of nodes that are the nodes traversed from root to this node.
This will help us finding the $K^{th}$ node from each node in every DFS call in $O(1)$ time
Update the answer for each DFS($u$) call considering $u$ as the starting interval of the chosen subset
answer = 0
parents = []
visited = [false] * N
function update_answer(starting_point):
# update answer
# based on the conditions
# mentioned above
function dfs(u):
parents.add(u)
update_answer(u)
visited[u] = true
for each neighbor v of u:
dfs(v)
parents.pop(u)
for i = N to 1:
if not visited[i]:
dfs(i)
print(answer)


