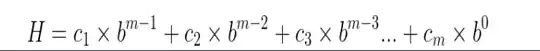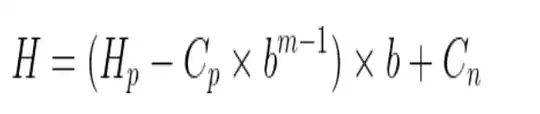How to use a worst case scenario in Rolling Hash: Rabin Karp Algorithm when the given string only contains the occurrences of "a and b?"

Question

Issue: I am having a hard time figuring out how to use the worst case for Rolling Hash, especially if the occurrences are only "a and b" for the string. Not only that but it is a bit of a hassle to figure out the process if the pattern that we tried to find from the given string will only contain one character occurrence, such as "bbbb".

How Rolling Hash is used in our class with a given formula and its process of solution:

Formulas:

Full document: https://drive.google.com/file/d/1vJr2UoFP7w2DFsJF9A5TmvHsoY9Zs3Iy/view?usp=sharing

The exercise problem that I am answering:

Given the following string and pattern. Determine the transition of the string comparison and hash value
when rolling hash or Rabin Karp algorithm is applied.
String = aabbaabbabbabababbbbbbaaaa
The following patterns that we need to find are:

bbbb
baaaa
bbab

My attempt for pattern "bbbb" by using the "String = aabbaabbabbabababbbbbbaaaa":

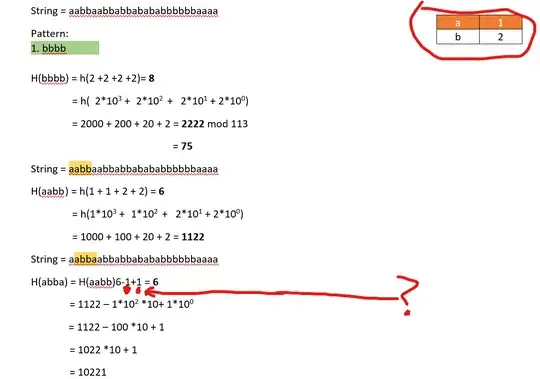
Not picture form:

String = aabbaabbabbabababbbbbbaaaa
Pattern:
1. bbbb
H(bbbb) = h(2 +2 +2 +2)= 8
                = h(  2103 +   2102  +   2101 + 2100)
                = 2000 + 200 + 20 + 2 = 2222 mod 113
                  = 75

String = aabbaabbabbabababbbbbbaaaa

H(aabb  ) = h(1 + 1 + 2 + 2) = 6

                = h(1103 +   1102  +   2101 + 2100)
                = 1000 + 100 + 20 + 2 = 1122

String = aabbaabbabbabababbbbbbaaaa

H(abba) = H(aabb)6-1+1 = 6

               = 1122 – 1102 10+ 1100 
                      = 1122 – 100 10 + 1

               = 1022 *10 + 1
               = 10221

I am now quite unsure with the -1 and +1 that I have annotated, in which these values involve the character present from the previous pattern but is now absent from the current pattern( - 1(where a is 1), and +1 where it is the character found from the current pattern but is absent to the previous pattern(still a).

I considered these a's because of their specific position being different, thus for me, they are considered somewhat missing/unique in comparing between two patterns.

Am I doing the process right or should I not consider these conditions? Especially since the string patterns both contain only the occurrences of a and b as we traverse in finding the exact pattern into the given string that we are using.

I decided to stop the process first since I might be doing it wrong, especially since it may take a while to find the exact pattern string.

Your response would indeed help me a lot! Thank you very much!!!

Answer 1

A clearer explanation

Let $\beta$ be a positive integer. ($b$ will be used as a character)

Let string $s=c_1c_2\cdots c_m$. Then $$H(s) = c_1\times \beta^{m-1} + c_2\times \beta^{m-2} + c_3\times \beta^{m-3} + \cdots + c_m\times \beta^0$$ where we abuse $c_i$ to also denote the number that encodes it. For example, $a=1$, $b=2$, etc.

$$\text{TEXT:}\quad**********\, \rlap{\,\overbrace{\phantom{C_{\text{prev}}*********\,}}^{\text{previous window}}} C_{\text{prev}}\,\underbrace{**********C_{\text{next}}\!}_{\text{next window}}************* $$

$$H_{\text{next}}=(H_{\text{prev}}-C_{\text{prev}}\times \beta^{m-1})\times \beta + C_{\text{next}}$$ where $*$ stands for a character. Each window consists of $m$ characters.

---

Let $m=4, \beta= 10$.
Pattern: $bbbb$

$$\begin{aligned} H(bbbb) &= 2*10^3 + 2*10^2 + 2*10^1 + 2*10^0\\ &= 2000 + 200 + 20 + 2\\ &= 2222 \end{aligned} $$ String = $aabbaabbabbabababbbbbbaaaa$
$$\begin{aligned} H(aabb) &= 1*10^3 + 1*10^2 + 2*10^1 + 2*10^0\\ &= 1000 + 100 + 20 + 2\\ &= 1122\\ H(abba) &= H(\not {\! \color{red}a} abb\color{blue}a)\\ &=(H(\color{red}aabb) - \color{red}a *10^3) * 10 +\color{blue}a\\ &= (1122 - \color{red}1*1000) * 10 + \color{blue}1\\ &= 1221 \\ H(bbaa) &= H(\not {\! \color{red}a} bba\color{blue}a)\\ &=(H(\color{red}abba) - \color{red}a *10^3) * 10 +\color{blue}a\\ &= (1221 - \color{red}1*1000) * 10 + \color{blue}1\\ &= 2211 \\ H(baab) &= H(\not {\! \color{red}b} baa\color{blue}b)\\ &=(H(\color{red}bbba) - \color{red}b *10^3) * 10 +\color{blue}b\\ &= (2211 - \color{red}2*1000) * 10 + \color{blue}2\\ &= 2112 \end{aligned}$$

$\newcommand{\m}{\operatorname{\%}}$

Shrink hash by $\m$

When $m$ is as big as 100 or even bigger, the hash can be too large to be operation friendly. We can shrink the hash by taking its remainder after dividing a fixed positive integer, i.e., modulo that fixed number.

Let us run all above again, with $\m d$ inserted, where $d$ is a positive integer.

$$H(c_1c_2\cdots c_m) = (c_1\times \beta^{m-1} + c_2\times \beta^{m-2} + c_3\times \beta^{m-3} + \cdots + c_m\times \beta^0)\m d$$

$$H_{\text{next}}=((H_{\text{prev}}-C_{\text{prev}}\times \beta^{m-1})\times \beta + C_{\text{next}})\m d$$ where $*$ stands for a character. Each window consists of $m$ characters.

---

Let $m=4, \beta= 10, d = 113$.
Pattern: $bbbb$

$$\begin{aligned} H(bbbb) &= (2*10^3 + 2*10^2 + 2*10^1 + 2*10^0)\m113\\ &= (2000 + 200 + 20 + 2)\m113\\ &= 2222 \m113 \\ &= 75 \end{aligned} $$ String = $aabbaabbabbabababbbbbbaaaa$
$$\begin{aligned} H(aabb) &= (1*10^3 + 1*10^2 + 2*10^1 + 2*10^0)\m113\\ &= (1000 + 100 + 20 + 2)\m113\\ &= 1122\m113\\ &= 105\\ H(abba) &= H(\not {\! \color{red}a} abb\color{blue}a)\\ &=((H(\color{red}aabb) - \color{red}a *10^3) * 10 +\color{blue}a))\m113\\ &= ((105 - \color{red}1*1000) * 10 + \color{blue}1) )\m113\\ &= -8949\,\m113 \\ &= 91\\ H(bbaa) &= H(\not {\! \color{red}a} bba\color{blue}a)\\ &=((H(\color{red}abba) - \color{red}a *10^3) * 10 +\color{blue}a)\m113\\ &= ((91 - \color{red}1*1000) * 10 + \color{blue}1))\m113\\ &= -9089\m113 \\ &= 64 \\ H(baab) &= H(\not {\! \color{red}b} baa\color{blue}b)\\ &=(H(\color{red}bbba) - \color{red}b *10^3) * 10 +\color{blue}b)\m113\\ &= ((64 - \color{red}2*1000) * 10 + \color{blue}2)\m113\\ &= -19358 \m113 \\ &= 78 \end{aligned}$$

Answer 2

You can build a quick intuition by considering digit-only string and using the decimal value of the substring as its hash. Let's find substring "345" in string "123456789".

At the first pos, we have hash 1*100+2*10+3 = 123. At second, 234. And at third, 345.

In the same way, you can find for example "333" in "1233345".