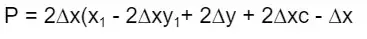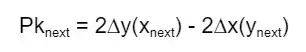How is slope error calculated for Bresenham’s Algorithm for both 2D and 3D?

Question

I've been working with Bresenham’s Algorithm in 2D and understand it is derived from the following logic:

y = mx+c

To get the slope error at a given point, the following equation is used:

d2 is the distance from value Y to the whole integer above. d1 is the distance from value Y to the whole integer below.

d1 - d2 = [m(xₖ+1)+c - yₖ]-[yₖ+1-m(xₖ+1)+c]

If d1 - d2 < 0, the next pixel should be (xₖ+1, yₖ)
If d1 - d2 >= 0, then the next pixel should be (xₖ+1, yₖ+1)

This gets turned into and reduce to the following equation to remove the m variable.:

Pk = 2∆y(xₖ) - 2∆x(yₖ) + 2∆y + 2∆xc - ∆x

The initial value of the error is:

c = y1 - (∆y/∆x)*x₁

With the loops step increasing this decision value by:

The actual value of next is calculated by plugging in (xₖ+1, yₖ+1) and (xₖ+1, yₖ) and subtracting Pknext - Pk. If this value is less than zero, we choose (xₖ+1, yₖ).

When (xₖ+1, yₖ+1) and (xₖ+1, yₖ) are plugged into Pknext, they end up simplifying to 2(∆y-∆x) and 2∆y.

This simplifies this logic into:

Constraints
x₁ < x₂
y₁ < yx₂
∆y/∆x ≤ 1
Given x₁, y₁, x₂, y₂ 
∆x = x₂ - x₁
∆y = y₂ - y₁
P = 2∆y - ∆x # Inital Decision value
while x ≤ x₂
    x = x+1
    IF P  < 0
        Plot(x,y)
        P  = P + 2∆y # Decision value of East
    ELSE
        Plot(x,y+1)
        P  = P + 2∆y - 2∆x # Decision value of North East

How is this logic applied in 3D?

I found this article by geeks for geeks: https://www.geeksforgeeks.org/bresenhams-algorithm-for-3-d-line-drawing/

But it never explained how the math is derived. We can get the value of Y by simply using mx+b and calculating the decision variable from there, but how is the decision variable done in 3D?

score 1 · Accepted Answer · 2022-07-27T20:03:10.590

I will first explain a closely related line drawing algorithm in 2D.

The parametric equation of a continuous line can be written vectorially

P = P0 + t.∆P

where t runs from 0 to 1.

If we want to discretize in such a way that the pixels are contiguous, the increment of t must be the smallest of 1/∆x and 1/∆y, let 1/∆, and we compute the points

Pi = P0 + i.∆P/∆.

Assuming that ∆=∆x, this is

Pix = P0x + i
Piy = P0y + i.∆y/∆x.

(i runs from 0 to ∆x)

For efficiency, the division of i.∆y by ∆x can be done incrementally by keeping the quotient and the remainder (i.∆y = q.∆x + r); for a new i, we add ∆y to the remainder and if it exceeds ∆x, we fix by subtracting ∆x and incrementing the quotient. This explains the if statement in Bresenham, which chooses between a lateral (east) or diagonal (north-east) move.

x+= 1 // East
r+= ∆y
if r ≥ ∆x
    r-= ∆x; y+= 1 // North

Now the generalization to 3D is immediate: choose ∆ = max(∆x, ∆y, ∆z) and, assuming ∆=∆x,

Pix = P0x + i
Piy = P0y + i.∆y/∆x
Piz = P0z + i.∆z/∆x.

A complete discussion must involve the signs of the deltas.

How is slope error calculated for Bresenham’s Algorithm for both 2D and 3D?

1 Answers1