What is the correct way to draw NFA of RE (a|b|c)?

Question

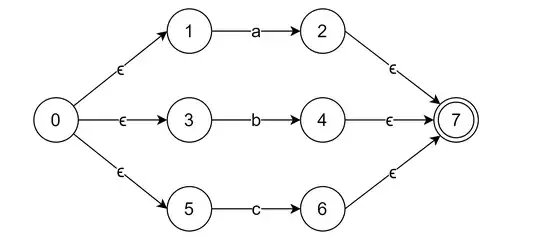
We were assigned to draw NFA for regular expression a|b|c, so like any one I draw this

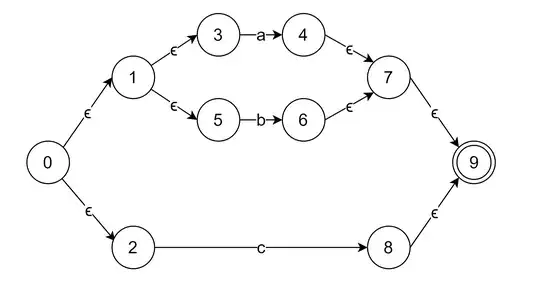
But my professor told me it is wrong, the correct way is

So, I checked it on online tools toolbox by cyberzhg, and regexper and according to both of them I am also correct.

Professor's argument was in maths for 4+5+1, we first add either 4+5 or 5+1 together then we add result of it with the remaining number. That is why for a|b|c, the correct solution is either (a|b)|c or a|(b|c).

Can you please tell are we both correct?

Answer 1

There is no unique way of converting a regex into NFA. That is, for any regular language $L$ there exist multiple (even, infinite) number of NFAs that accept the language $L$.

The solution of your professor restricts each state to have at most 2 outgoing states, while your solution does not. Unless this restriction was required by the professor somehow, both solutions are equivalent in the sense they both accept the language $L=\{a, b, c\}$ defined by the regexp a|b|c.

Note, that the professor might wanted you to work in methodological way, where there are fixed "gadgets", i.e., converting x|y to some certain states, and converting xy to other (fixed) states. Then, their comment makes sense - they wanted you to interpret a|b|c as (a|b)|c, first use the gadget on a|b to obtain the upper half of the machine, and then use the gadget again on x|c where $x$ is the already-constructed machine. If this (or any fixed other) methodology was required, then the outcome NFA would be unique.