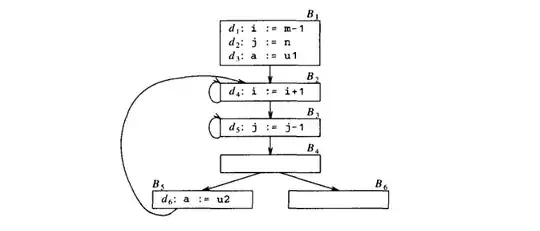
I was going through the concept of reaching definitions from the red dragon book.
The authors define reaching definitions as follows:
Definition: We say a definition $d$ reaches a point $p$ if there is a path from the point immediately following $d$ to $p$, such that $d$ is not "killed" along that path.
Then the authors consider a flow graph and explain the definition with an example as follows:
For example, both the definitions
i:=m-1andj:=nin block $B_1$ in Fig. above reach the beginning of block $B_2$, as does the definitionj:=j-1, provided there are no assignments to or reads ofjin $B_4$, $B_5$, or the portion of $B_3$ following that definition.
I can understand that in $B_4$, $B_5$, or the portion of $B_3$ following that definition j:=j-1 if there is an assignment to j then the definition $d_5$ is killed. But what problem shall be there if there is simply a read of the value j? How does it kill the definition $d_5$ and prevent it from reaching the top of $B_2$?