How to score a given arrangement of windows on a screen to produce good layouts

Question

(this is related to my other question, see here)

I would like to write a function that scores a given arrangement of windows on a screen.

The purpose of this function is to determine whether a particular layout is good and by going over other possible layouts, finding the one with the highest score.

Here are some characteristics that I think make a good layout:

1. maximizing amount of space used by windows (or in other words, the free space on the screen should be minimized)
2. windows are (more or less) evenly sized

Bonus: assigning each window a priority and giving a higher score for layouts where windows with a higher priority take more space.

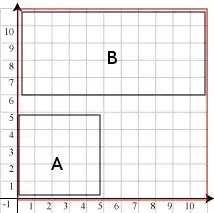
Here's an example: Suppose our screen is 11x11 and we want to put two windows on it. Window A's initial size is 1x1 and window B is 2x1.

When we resize windows, we preserve their aspect ratio. So here are two possible layout:

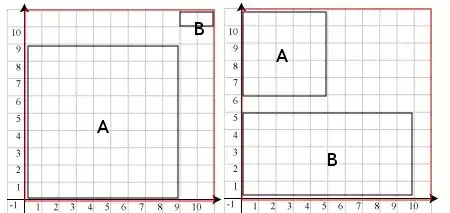
The function should give the one on the right a higher score.

Another nice thing to have is the option to 'dock' a window to one or more sides of the screen. Then suppose we want to dock A to the bottom-left of the screen, the scoring function should prefer this layout than the above one on the right:

Answer 1

I will expand on my comment on the other question and propose a target function that ensures that no very small windows occur and that windows are not unnecessarily far away from screen edges. Let $\mathcal{W} = \{1,\dots,n\}$ a set of windows and $T = \mathcal{W} \to \mathbb{N}^4$ a tiling; if $T(W) = (x,y,w,h)$ window $W$'s top-left corner is positioned at $(x,y)$ and $W$ has width $w$ and height $h$. Now let $c : (\mathbb{N}^4)^\mathcal{W} \to \mathbb{R}$ a cost function from the space of all tilings to the reals:

$\qquad \displaystyle c(T) = \left[ \min_{W \in \mathcal{W}} T(W)_3\cdot T(W)_4 \right] - \sum\limits_{W \in \mathcal{W}} \operatorname{empty}(W)$

where $\operatorname{emtpy}(W)$ the maximum number of empty tiles between one of $W$'s edges and the respective nearest screen edges. The objective is maximisation.

Note that this is a (non-equivalent) simplification of the multicriteria optimisation goal of maximising

$\qquad \displaystyle c(T) = \left( \min_{W \in \mathcal{W}} T(W)_3\cdot T(W)_4 \ ,\ -\sum\limits_{W \in \mathcal{W}} \operatorname{empty}(W)\right)$.

Of course you need appropriate restrictions in place that ensure that now window is placed outside of the screen and windows do not overlap.