Is the language of words containing equal number of 001 and 100 regular?

Question

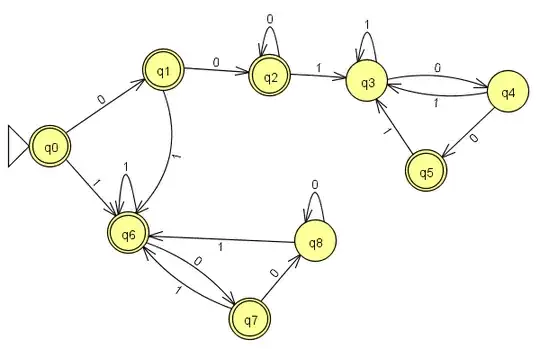
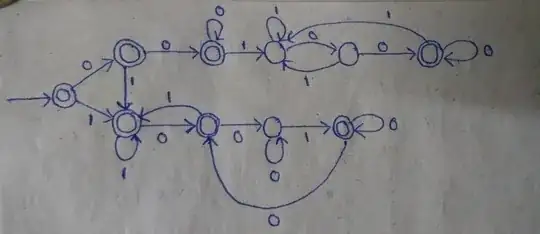
I was wondering when languages which contained the same number of instances of two substrings would be regular. I know that the language containing equal number of 1s and 0s is not regular, but is a language such as $L$, where $L$ = $\{ w \mid$ number of instances of the substring "001" equals the number of instances of the substring "100" $\}$ regular? Note that the string "00100" would be accepted.

My intuition tells me it isn't, but I am unable to prove that; I can't transform it into a form which could be pumped via the pumping lemma, so how can I prove that? On the other hand, I have tried building a DFA or an NFA or a regular expression and failed on those fronts also, so how should I proceed? I would like to understand this in general, not just for the proposed language.

Answer 1

An answer extracted from the question.

Yes, it is regular; below is an automaton that accepts it.

As pointed out by Hendrik Jan, there should be an additional 0 self-loop at q5.

Answer 2

It's a trick question. Try constructing a string that contains two 001 and doesn't contain a 100, and see why you can't do it. If X = "number of 001", and Y = "number of 100", then X = Y or X = Y ± 1.

Once you realise the trick, it becomes highly unlikely that the language is irregular, and then constructing a DFA is quite simple. There are only 8 states with their transitions if the next symbol is 0/1:

State S0: Input is empty. -> S1/C0

State S1: Input is 0. -> C2/C0

State A: Y = X + 1, input ends in 00. -> A/C0

State B0: X = Y + 1, input ends in 1. -> B1/B0

State B1: X = Y + 1, input ends in 10. -> C2/B0

State C0: X = Y, input ends in 1. -> C1/C0

State C1: X = Y, input ends in 10. -> A/C0

State C2: X = Y, input ends in 00. -> C2/B0

The initial state is S0, and S0, S1, C0, C1, C2 are accepting states.

Answer 3

We can write every string in $\{0,1\}^*$ in the form $$ 0^{i_0} 1 0^{i_1} 1 0^{i_2} \cdots 0^{i_{m-1}} 1 0^{i_m} $$ Here $i_j \geq 0$, and $m$ is the number of $1$s.

The number of copies of $001$ is the number of indices $i_0,\ldots,i_{m-1}$ which are at least $2$.

The number of copies of $100$ is the number of indices $i_1,\ldots,i_m$ which are at least $2$.

We conclude that the number of copies of $001$ is the same as the number of copies of $002$ iff $$ i_0 \geq 2 \Leftrightarrow i_m \geq 2. $$ This leads to the following regular expression: $$ 0^* + (\epsilon+0)(10^*)^*1(\epsilon+0) + 000^*(10^*)^*1000^*. $$

Answer 4

$L=\{\epsilon, 0, 1, 01, 10, 010, 101, 00, 000, 0000,..... , 1, 11, 11111,......, 01110, 1001, 00100,.........\}$ The pattern I can observe here is whenever we see a '001' as a substring then it has to be followed by 00 to make $n(001)=n(100)$ and whenever we see '100' as a substring then it has to be followed by 1 to make it '1001' to make $n(100)=n(001)$

Answer 5

Several years ago I and several colleagues generalized when the language of all strings with equal number of $x$ and $y$ substrings over an alphabet $\Sigma$ is regular: https://arxiv.org/abs/1804.11175. The condition depends on whether $x$ is "interlaced" by $y$ or vice versa. For $x$ to be "interlaced" by $y$, it must be the case that $x$ is a substring of every string in $\Sigma^\star$ that starts and ends with $y$. We also give a construction whenever the condition is satisfied.

In the case of $x=001$ and $y=100$ over $\Sigma = \{0,1\}$, every string that starts and ends with $y=100$ must have the form $100\cdots100$. No matter what, $x=001$ is a substring of it. Therefore, this language is regular.