one-to-many matching in bipartite graphs?

Question

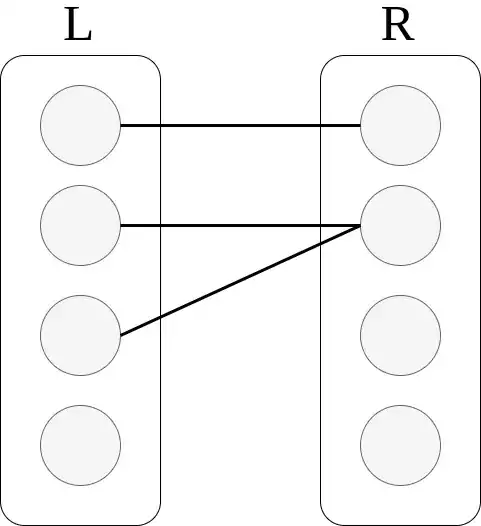
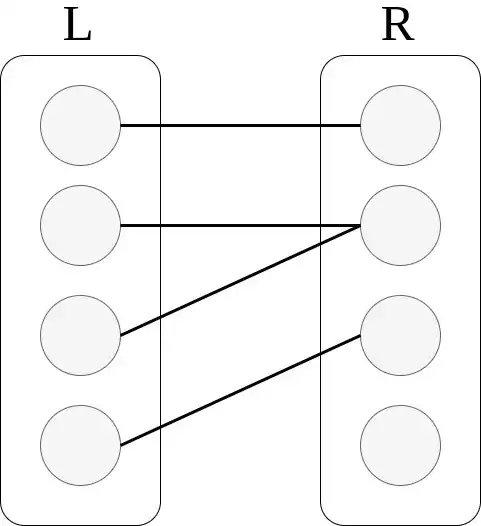
Consider having two sets $L$ (left) and $R$ (right). $R$ nodes have a capacity limit. Each edge $e$ has a cost $w(e)$.

I want to map each of the $L$ vertices to one node from $R$ (one-to-many matching), with minimum total edge-costs.

Each vertex in $L$ must be mapped to one vertex in $R$ (but each node in $R$ can be assigned to multiple $L$-nodes).

Examples: Consider the capacity of $R$ nodes is $2$.

1) This is NOT correct, since one node from $L$ has not assigned to a node in $R$.

2) This is NOT correct, since the capacity of a node in $R$ is violated.

3) This IS correct. All $L$ nodes are assigned to a node in $R$, and the capacity of $R$ nodes is not violated.

Any idea how can I solve this?

Answer 1

This problem is called the B-matching problem. Where you are given a function $b:V \rightarrow \mathbb{N}$ that assign a capacity to each vertex and a function $u:E \mapsto \mathbb{N}$ that assigns a weight to each edge.

The problem is solvable in polynomial time. An easy solution is to reduce the problem to minimum weight maximum matching. Create $b(v)$ copies of each vertex $v$ and connect each of them to all neighbors of the original vertex v. We get a polynomial time reduction, since for $b(v) \geq \mathrm{deg}(v)$ we can set $b(v) := \mathrm{deg}(v)$ since we can not match $v$ with more vertices than its neighborhood anyway and that each of its neighbors is matched with at most one vertex in your special case.