Merging nodes of a DAG

Question

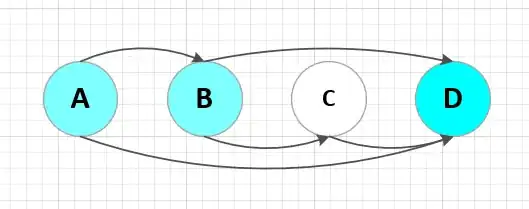
I would like to merge connected nodes with a specific attribute of a directed acyclic graph. The purpose is to detect max connected clusters of blue nodes and merge them. After each merge operation, the graph should remain acyclic. Let's say my graph contains blue nodes and white nodes.

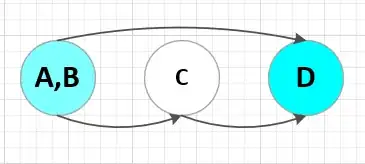
A and B are connected, they may be merged:

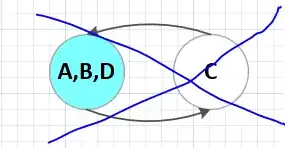
The above graph is DAG. Merging node {A,B} with node {D} is illegal since it creates a cycle!

My current algorithm is based on union-find.

For each blue node b:
   Make-Set(b)
For each two connected blue nodes a,b: 
   Union(a,b)
For each set://Created at the previous step
   merge all nodes of the set

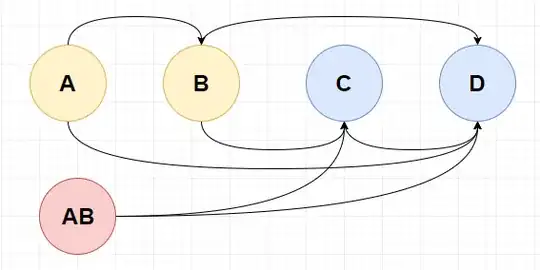
The bug is the output graph contains cycles. How can I avoid merges that create cycles in the graph? Before each Union, I need to check that it "safe". Safe means that after merging cycle will not be created. I can find all passes between the set of a and set of b before Union but this solution is too expensive (time complexity). I can't use solutions with a quadratic time complexity since my graph is too big. Edit: We can merge nodes according to topological order but the following case will be messed (D):

Nodes A, B, and D may be merged, but we will merge only A and B. Max Cluster example: at the graph below the cluster is {A, B, C, D, E}

score 1 · Answer 1 · answered Aug 18 '19 at 14:21

I think instead of performing merge at the beginning. We can add a node which has the similar edges as the two merged vertices.

Having the following DAG.

If we want to merge node A and B. We add a new node which has the similar attributes as A + B.

Then trasverse from new node AB (should be Depth-first):

If it find Node A or B, then the merge should be cancelled because it creates a cycle. simply delete Node AB.
If we do not se Node A or B, the merge is valid so delete node A and node B.

Merging nodes of a DAG

1 Answers1