Can someone point out why these directed graphs aren't equivalence relations?

Question

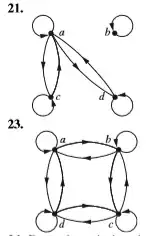
As far as I can tell, these two directed graphs are reflexive, symmetric and transitive.

Answer 1

In the first one we have c ~ a and a ~ d but not c ~ d, so the relation is not transitive. A similar problem exists for the other graph. See if you can find the issue yourself.

Then ask yourself what the graph of an equivalence relation looks like in general.

Answer 2

The answer is 23 because we can see that, the graph fulfills all the properties of an equivalence relationship whcih are reflexivity, symmetry and transitivity.