Relation between semi decidable, undecidable and countable sets

Question

I know that

• decidable problem: has both counting (bijection with $\mathbb N $) and membership algorithm (TM halts for both member and non member strings )
• semidecidable problem: has counting algorithm and TM halts for member strings
• countable problem: has only counting algorithm

Now I have come across undecidable language set which does not have membership algorithm (as semi decidable languages at least have TM which halts for member strings, which is not the case for undecidable problems), that is it does have TM that halt neither for member string nor for non member string.

I have doubt about the relationship between these language classes.

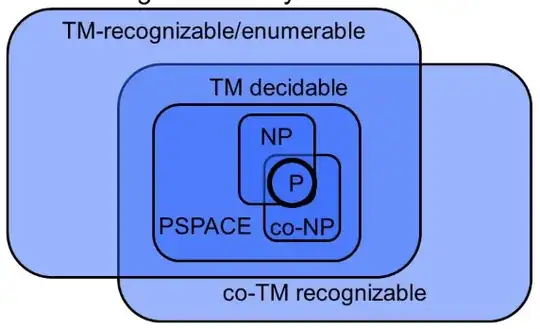
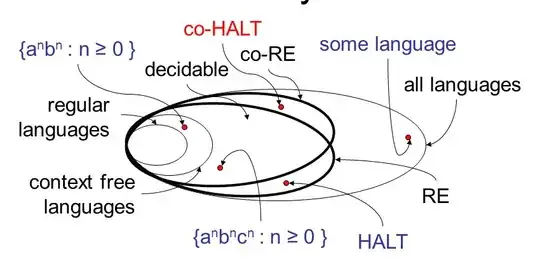
I know "decidable $\subset$ semi decidable $\subset$ countable".

Where does "undecidable" fit here?

Is it like this?:

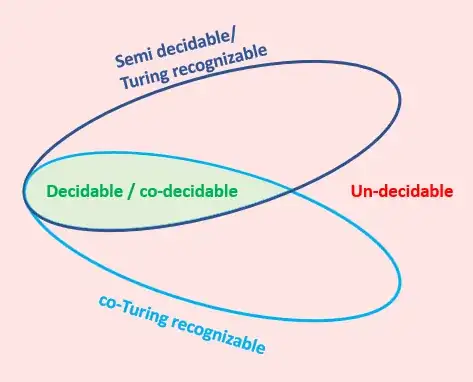
(Match the color of text with that of the border. Region color is lighter shades of corresponding enclosed texts.)

Q. Is above diagram correct? Also I want to add "countable" to above. I feel, for finite alphabet languages, countable will be proper superset of "undecidable". Is it right?

PS: I feel, earlier I based my understanding of "undecidable" on incorrect definition given in this question. So I draw wrong diagram earlier. I believe its correct now.

Answer 1

Undecidable is simply the complement of decidable, as the name suggests: anything that is not decidable is undecidable. So the whole pink area of your diagram consists of undecidable languages.

All languages over finite alphabets are countable. For example, every string over alphabet $\{0,1\}$ is a natural number written in binary.¹ Everything in your diagram is countable. We only ever consider finite alphabets; infinite alphabets aren't physically realizable because we can't store infinitely many distinguishable possibilities in a finite space.

---

^{1. A small problem is that $0$, $00$, $000$, etc. are all the number zero written in binary. So, instead, associate the binary string $xyz$ with the natural number $1xyz$ and now, every binary string represents a different natural number.}

Answer 2

A language is defined as a set of strings over an alphabet. We will assume the usual situation where the alphabet is a finite set. Then the set of all strings are countably infinite. Why is it countable? Because we can list all strings of length 0, all strings of length 1, all strings of length 2, all strings of length 3 and so on.

The correct diagram should look like the following (where we assume P!= NP), where the enclosing unlabeled plane represents languages that are countable. Note all languages that sit outside of the region of "TM decidable" is "TM undecidable". Note that we usually say "decidable", "recognizable", "co-recognizable" and "undecidable" simply without the prefix "TM".

For completeness, we have the following diagram that includes chomsky hierarchy.