Optimal dividing of K people into N groups

Question

A teacher at a school has to do this on a regular basis. Let's say 12 students should be divided into either 4 groups of 3, or 3 groups og 4. Each student can pick up to 3 other students that person would most rather be with.

I tried to set this up as an undirected weighted graph, and implement shortest path algorithms, but the shortest path here doesn't ensure that as many students as possible get their top wish.

What algorithm should I look into here, in order to achieve to most optimal solution to a problem like this?

Here is a visualisation of the problem:

OzrenTkalcecKrznaric · Accepted Answer · 2019-01-17T16:46:10.437

Solution in pseudocode:

initialize collection of persons (e.g. an array): 
    - each person itself is described by its position in collection
    - each person itself contains collection of positions (e.g. an array) 
      that describe wished persons for the person to be grouped with
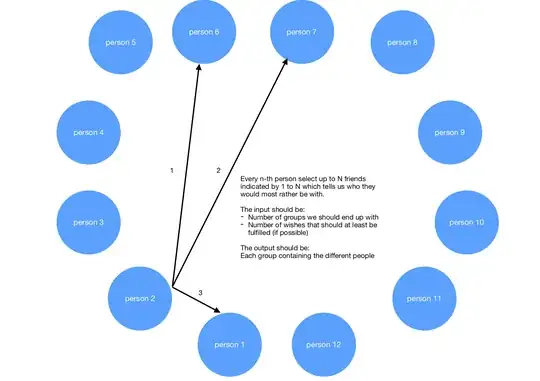
(example: persons = [[1,2], [0,2], [0,3], [0,2]])

initialize empty collection of groups (e.g. an array): 
    - each group itself is described by its position in collection
    - each group itself contains collection of positions (e.g. an array) 
      that describe grouped persons

initialize number of persons per group (example: 2)
initialize total group count to be number of persons divided by number of persons per group (example: 2)
initialize constraint c1 as: any group shouldn't exceed the number of persons per group
initialize constraint c2 as: group count shouldn't exceed the number of total group count
initialize constraint c3 as minimum required of wishes granted per person in any group, for the solution to be valid (example: 1)
[*]initialize dictionary of solutions, where key is a pair (persons, groups), and value is a solution or an empty value

call group(persons, groups)

procedure group(persons, groups):
    [*]if there is a pair (persons, groups) in dictionary of solutions
    [*] return that solution

    for each person (let's call it this-person)
        for each person among this-persons wishes (let's call it wished-person)
            if wished-person is already grouped in any of the groups
                if this-person can be grouped in the same group with wished-person, at the same time satisfying c1
                    set new-groups as groups with this-person grouped accordingly
                    set new-persons as persons without this-person
                else
                    nothing can be done with wished-person, so continue with the next wished-person
            else
                if both this-person and wished-person can be grouped in any group, at the same time satisfying c1 and c2
                    set new-groups as groups with this-person and wished-person grouped accordingly
                    set new-persons as persons without both this-person and wished-person
                else
                    nothing can be done with wished-person, so continue with the next wished-person

            if there are any other persons left in new-persons
                set possible-solution to recursive call, group(new-persons, new-groups)
                if possible-solution is not empty 
                    [*]add item to dictionary of solutions, key is the pair (persons, groups), value is possible-solution
                    return it as a solution
            else if all the groups satisfy c3
                return new-groups as the solution

    [*]add item to dictionary of solutions, key is the pair (persons, groups), value is empty
    return empty value

The decision tree will exhaust all the possible paths towards the solution. However, if you use dynamic programming you can improve the performance by avoiding the execution of already known paths. The dynamic-programming part is marked with [*] in pseudocode.

You might further improve the performance by preferring least-popular persons over most popular when grouping.

Here's a Python implementation in case anyone needs it: https://repl.it/@OzrenTkalcec/Dividing-of-K-people-into-N-groups

Disclaimer: I'm not a data scientist, but I like to solve puzzles like this one :)

HTH

Optimal dividing of K people into N groups

1 Answers1